PUCRIO – Física 3 2020.2 – G4 – Questão 3
Muito tempo após o fechamento da chave , ela é aberta e, simultaneamente, apenas a chave é fechada, dando início à FASE 2 (a chave continua aberta). Observou-se que a corrente no circuito relevante varia em função do tempo (medido em segundos a partir do início da FASE 2) de acordo com a expressão , sendo e , tendo sentido consistente com o determinado no item (a). Observe que resulta da derivada em relação ao tempo da expressão para a carga no capacitor C1: . Com base nestas informações:
c) Determine os valores de e .
d) Determine o valor do módulo das cargas iniciais no capacitor , indicando se a carga positiva está na sua placa superior ou inferior.
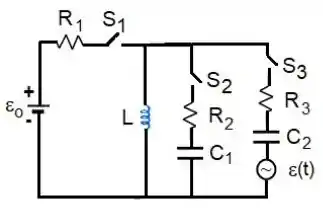
Passo 1
Fala galera, tudo bem? Vou ajudar você aqui!
Letra (c):
Da equação dada para a fase temos a seguinte comparação:
Daí usando o valor de e , podemos achar :
E agora a freqüência angular. Temos a seguinte relação para esse circuito:
Queremos saber o valor de (para achar a capacitância ), substituindo os valores temos:
E daí da freqüência :
Passo 2
Letra (d):
A primeira expressão e o resultado do item (a) – os valores de e , bem como a energia armazenada no indutor - dessa questão mostram que , daí a carga máxima é:
Pela nossa convenção, o sentido positivo da corrente é do terminal positivo para o negativo. Como a corrente tem sentido de baixo para cima no capacitor (portanto no mesmo sentido da corrente inicial no indutor ), seu terminal positivo é o inferior. No entanto, a segunda expressão indica que , indo de encontro à convenção.
Sendo assim, a carga inicial está na placa superior do capacitor .
Beleza?
Espero ter te ajudado!