A figura abaixo mostra as linhas do campo eletrostático produzido por um par de partículas de cargas e . A figura mostra ainda duas superfícies imaginárias e fechadas, e , indicadas pelas linhas tracejadas. A superfície envolve apenas a partícula de carga , enquanto envolve as duas partículas. Considere que o vetor normal a estas superfícies aponta para fora delas, seguindo a orientação usual. Sobre essa situação, considere as afirmativas abaixo:
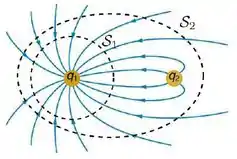
(I) O fluxo de campo eletrostático através de vale .
(II) O fluxo de campo eletrostático através de é negativo.
(III) O fluxo de campo eletrostático através de é nulo.
São VERDADEIRAS as afirmativas:
(a) Apenas I
(b) Apenas II
(c) Apenas III
(d) Apenas I e II
(e) Apenas I e III
(f) Apenas II e III
(g) I, II e III
(h) Nenhuma delas
Passo 1
Vamos analisar cada uma das afirmativas:
I) Falso. A carga interna em é apenas , logo, não faria parte da expressão.
II) Verdadeiro. Em uma superfície fechada, o fluxo que aponta para dentro é negativo e o que aponta para fora é positivo. No caso de , temos apenas fluxo apontando para dentro da superfície.
III) Falso. Como dito na afirmativa anterior, temos apenas fluxo apontando para dentro em também, logo, ele é negativo e não nulo.
Portanto, a alternativa correta é a letra B.
Resposta
B) Apenas II