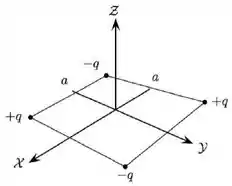
Quatro partículas carregadas são fixadas sobre os vértices de um quadrado de lado , como mostrado na figura abaixo. Duas delas possuem carga e as outras duas possuem carga . Este quadrado encontra-se sobre o plano , com seu centro sobre a origem e seus lados paralelos aos eixos e . O eixo é perpendicular ao plano do quadrado e passa por seu centro. Sobre essa situação, assinale a alternativa CORRETA:
(a) O trabalho realizado pela força elétrica ao trazer as quatro partículas do infinito até a configuração indicada na figura é nulo.
(b) O campo elétrico resultante produzido pelas quatro partículas tem a mesma intensidade em todos os pontos do eixo .
(c) O campo elétrico resultante produzido pelas quatro partículas é nulo em todos os pontos do eixo .
(d) A força elétrica resultante sobre qualquer uma das partículas devido às outras três é nula.
(e) Uma partícula carregada abandonada do repouso sobre o centro do quadrado entrará em movimento devido à ação de uma força elétrica.
Passo 1
Nesse caso, temos 5 alternativas sobre o sistema mostrado na figura e apenas uma delas está correta, então, a melhor opção é vermos as mais prováveis de acordo com a teoria vista e testarmos.
Vamos começar testando a alternativa A.
O trabalho da força elétrica pra trazer essas cargas do infinito até essa configuração é dado por
Onde é o potencial dessas cargas quando elas estão infinitamente afastadas. A energia dessa configuração é dada por
Onde temos que somar as interações entre todas as cargas.
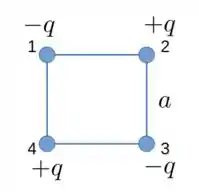
Então o trabalho pra construir essa configuração é dado por
Que é diferente de , ou seja, essa opção está errada!
Passo 2
Agora vamos olhar a opção B. Ela diz que o campo elétrico resultante tem a mesma intensidade em todos os pontos do eixo . Vamos pegar dois pontos, um em e outro em e vamos desenhar os campos como a figura abaixo
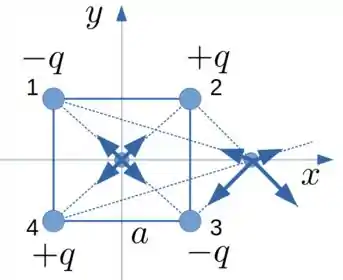
Em o campo resultante vai ser nulo. Já em o campo vai ser diferente de isso por que as cargas do lado direito estão mais próximas desse ponto do que as cargas do lado esquerdo, então os campos das cargas do lado direito é maior do que os campos produzidos pelas cargas do lado esquerdo.
Então essa opção está incorreta também!
Passo 3
Na alternativa C, ele nos diz que o campo elétrico resultante em qualquer ponto do eixo vai ser 0.
Vamos começar lembrando que o campo elétrico é dado por
Sendo o vetor unitário que é diretor da carga até o ponto do eixo z.
Sabendo que vai ser a distância da carga até o ponto do eixo , chegamos que
Vamos calcular o campo elétrico gerado por cada uma das cargas, numerando de acordo com a imagem.
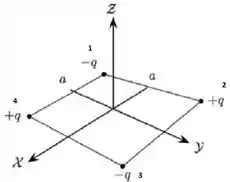
Esses campos elétricos são mostrados vetorialmente pela figura abaixo, em um ponto arbitrário do eixo .
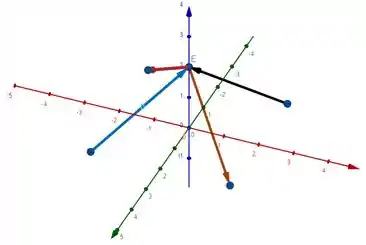
Por soma vetorial, concluímos que a resultante desses vetores é 0.
Isso por que as cargas no primeiro e no terceiro quadrantes fazem juntos uma força que aponta na direção e as cargas no segundo e quarto quadrante exercem juntas uma força na direção . Como todas as cargas estão à mesma distância desse ponto no eixo , a soma de todas as forças vai ser nula.
Então a alternativa C realmente está correta :D
Passo 4
Vamos olhar as outras pra ter certeza, beleza? Na letra D diz que a força elétrica resultante sobre qualquer uma das partículas devido às outras três é nula. Pra ver se é isso ou não vamos analisar as forças sobre uma das partículas
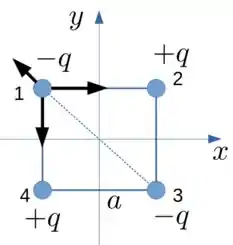
A força causada pela carga é dada por
Que aponta na direção da diagonal para fora.
Já as forças causadas pelas cargas 2 e 4, se somam e apontam na direção da diagonal apontando para o centro do quadrado. Como elas se somam e apontam na direção da diagonal, temos que projetar na direção da diagonal, ou seja, multiplicar pelo cosseno de 45
Como essas duas forças têm direções opostas e intensidades diferentes, a força sobre essa carga não é nula. Então essa opção é incorreta também :)
Passo 5
Vamos pra última! Ela diz que se abandonarmos uma partícula do repouso sobre o centro do quadrado ela começará a se movimentar devido a uma força elétrica. Já vimos que no centro do quadrado o campo elétrico é nulo! Então uma carga posta no centro do quadrado ficará parada já que a força resultante é nula.
Essa opção também está errada :)
Resposta
(C) O campo elétrico resultante produzido pelas quatro partículas é nulo em todos os pontos do eixo .