Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Capacitância Equivalente

Ver Teoria
Exercício 21123456789101112131415161718192022232425262728293031323334

Enunciado

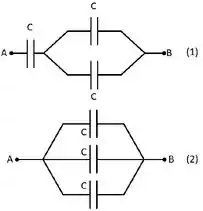
Considere os dois circuitos mostrados na figura abaixo. Todos os capacitores são idênticos e tem capacitâncias iguais a C . A diferença de potencial entre os terminais A   e B   também é a mesma. Sejam C 1 e C 2 as capacitâncias equivalentes dos circuitos 1 e 2 entre os terminais A e B , respectivamente. Nessa situação, podemos afirmar que a razão C 1 / C 2 vale:

(a) 9 / 2

(b) 2 / 3

(c) 3 / 2

(d) 4 / 9

(e) 2 / 9  

(f) 9 / 4

(g) 1

Passo 1

Temos no enunciado 2 circuitos distintos formados por capacitores. O que ele quer saber é qual é a razão entre as capacitâncias equivalentes do circuito 1 e do circuito 2.

A gente tem que lembrar que para capacitores em série, a capacitância equivalente é

C e q = C a C b C a + C b

Já para capacitores em paralelo, a capacitância equivalente vai ser

C e q = C a + C b

Aí nós calculamos a capacitância C 1 do circuito 1, a capacitância C 2 do circuito 2 e aí dividimos C 1 por C 2 :)

Passo 2

Primeiro bora calcular a capacitância do circuito 1. Lá a gente tem 1 capacitor em série com 2 capacitores em paralelo. Então vamos dividir assim:

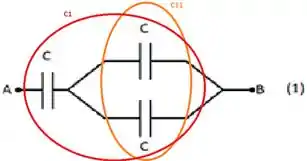
C 11 representa os dois capacitores em paralelo, então:

C 11 = C + C

C 11 = 2 C

C 1 é a associação em série de C com C 11

C 1 = C × C 11 C + C 11

C 1 = C × 2 C C + 2 C

C 1 = 2 C ² 3 C

Então a nossa capacitância equivalente do circuito 1 vale

C 1 = 2 C 3

Passo 3

No circuito 2, a gente tem 3 capacitores em paralelo, então a capacitância equivalente vai ser

C 2 = C + C + C

C 2 = 3 C

Passo 4

Agora é só a gente fazer C 1 / C 2

C 1 C 2 = 2 C 3 3 C

C 1 C 2 = 2 9

Então a alternativa correta é a letra E :D

Resposta

E) 2 / 9

Exercícios de Livros Relacionados

Na figura 25-96, V = 9,0 V, C 2 = 3,0 μF, C 4 = 4,0 μF e todos os capacitores estão inicialmente descarregados. Quando a chave S é fechada, uma carga total de 12 μC passa pelo ponto a e uma carga tota
Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica
Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e
Um átomo de U 238 tem massa de 3,97 × 10 - 22 g . Calcule a taxa de decaimento radioativo de uma amostra de um grama daquele isótopo, cuja vida média é 6,45 × 10 9 anos.
Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .