P1 de Física 3 da USP - 2010

Duas partículas puntiformes carregadas com a mesma carga positiva, fixas sobre o eixo , estão localizadas simetricamente em relação à origem, uma em e a outra em .

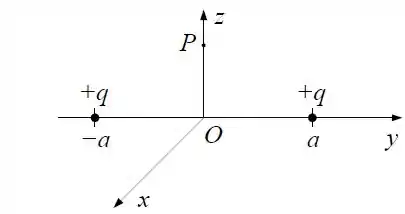
Determine o potencial eletrostático num ponto qualquer do espaço.

Suponha que uma partícula com carga seja abandonada do repouso no ponto com . Determine a energia cinética da carga quando ela passar pela origem do sistema de coordenadas (despreze a forca peso).

Calcule a energia potencial do sistema formado pelas três cargas na configuração em que a carga −Q está no ponto e na configuração em que a carga está na origem . O resultado é compatível com o obtido no item ?

Considere duas placas grandes, paralelas, a uma distância uma da outra, uma delas com densidade superficial de carga , uniforme, e a outra com densidade . Entre as duas placas paralelas é colocada uma chapa metálica de espessura , conforme mostra a figura.

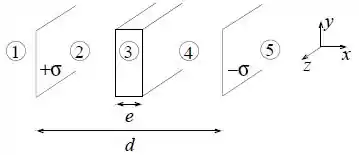
Demonstre que a intensidade do campo elétrico criado por um plano infinito com densidade superficial de carga é .

Utilizando o princípio de superposição e desprezando efeitos de borda, determine o vetor campo elétrico nas regiões e .

Se a chapa metálica for retirada da região entre as placas, haverá aumento ou diminuição da energia eletrostática do sistema? Justifique a resposta.

O potencial elétrico devido a uma esfera carregada de raio é

onde é constante e é a distância ao centro da esfera.

Determine o campo elétrico para e .

Determine a carga total da esfera.

Calcule o fluxo através da face superior do cubo de lados mostrado na figura que tem três arestas ao longo dos eixos e . Expresse o resultado em termos da carga total da esfera e de .

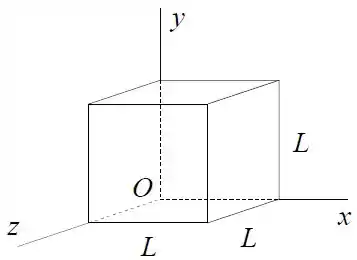
A densidade linear de carga ao longo do eixo é dada por:

onde e são constantes.

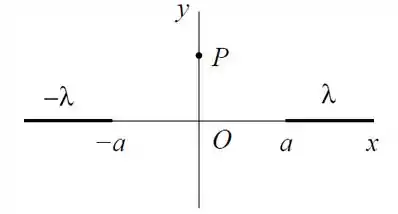
Calcule o campo elétrico num ponto sobre o eixo .

Adotando-se potencial nulo na origem , calcule o potencial num ponto sobre o eixo .

Considere os pontos , e . Qual é o trabalho efetuado pela força elétrica para levar uma carga q ao longo do percurso fechado ?