Densidade de Carga, Campos Elétricos e Corpos Carregados, Energia Potencial e Densidade de Energia, Potencial Elétrico
A densidade linear de carga ao longo do eixo é dada por:
onde e são constantes.
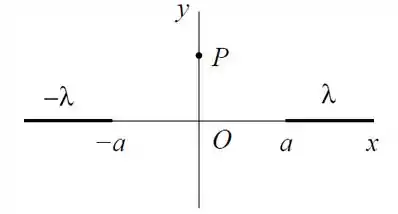
Calcule o campo elétrico num ponto sobre o eixo .
Adotando-se potencial nulo na origem , calcule o potencial num ponto sobre o eixo .
Considere os pontos , e . Qual é o trabalho efetuado pela força elétrica para levar uma carga q ao longo do percurso fechado ?
Passo 1
Calcule o campo elétrico num ponto sobre o eixo .
Beleza! O segredo aqui é começar escrevendo a e expressão do campo elétrico gerado por uma carga :
Como , nós podemos reescrever esse cara como:
Agora temos que levar em conta as duas linhas carregadas :
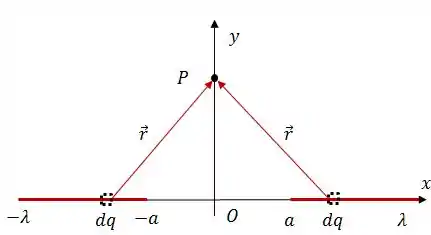
Daqui podemos tirar algumas coisas:
Além disso, para a linha da esquerda e, para o fio da direita, .
Substituindo na expressão de teremos:
O primeiro termo se refere ao fio da esquerda e o segundo se refere ao fio da direita.
Passo 2
Para encontrar a expressão do campo elétrico, basta integrar o primeiro termo de até e o segundo termo se até .
Eu sei que, olhando, essas integrais parecem ser muito chatas de resolver... e são. Mas elas aparecem frequentemente nesse tipo de problema, então vamos tentar dar uma simplificada nesse cara.
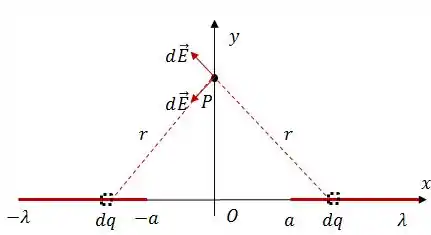
Decompondo os vetores, podemos ver que as componentes verticais se cancelam e as componentes horizontais se somam. Assim, podemos simplificar a expressão para , cancelando os termos verticais.
Logo:
Agora é só integrar esse cara. Ele pode ser resolvido com uma substituição simples.
Agora é só organizar esse cara.
Passo 3
Adotando-se potencial nulo na origem , calcule o potencial num ponto sobre o eixo .
Por definição, o potencial está associado ao campo elétrico por:
Como temos que calcular o potencial ao longo do eixo , . Substituindo e na expressão de , teremos:
Obs.: O resultado vai ser zero pois .
Passo 4
Considere os pontos , e . Qual é o trabalho efetuado pela força elétrica para levar uma carga q ao longo do percurso fechado ?
Como a força eletrostática é uma força conservativa, o trabalho para levar a carga ao longo de um caminho que começa e termina no mesmo lugar será nulo. Logo:
Resposta