O potencial elétrico devido a uma esfera carregada de raio é
onde é constante e é a distância ao centro da esfera.
Determine o campo elétrico para e .
Determine a carga total da esfera.
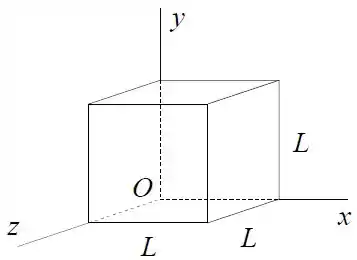
Calcule o fluxo através da face superior do cubo de lados mostrado na figura que tem três arestas ao longo dos eixos e . Expresse o resultado em termos da carga total da esfera e de .
Passo 1
Determine o campo elétrico para e .
Por definição, podemos associar o campo elétrico com o potencial por:
Então só temos que aplicar isso para os dois casos:
Passo 2
Determine a carga total da esfera.
Podemos usar a Lei de Gauss pra associar a carga total com o campo elétrico que nós já calculamos:
Como estamos falando de uma esfera, podemos simplificar a Lei de Gauss para:
Já que pretendemos calcular a carga da esfera, a nossa gaussiana deve ter um raio para que englobe toda a esfera. Logo:
Agora é só dar uma organizada:
Passo 3
Calcule o fluxo através da face superior do cubo de lados mostrado na figura que tem três arestas ao longo dos eixos e . Expresse o resultado em termos da carga total da esfera e de .
Por definição, o fluxo de campo elétrico é dado por:
E podemos associar o fluxo no cubo diretamente com a Lei de Gauss:
Logo:
Assim, temos agora que descobrir a carga englobada pelo cubo.
Como o a esfera de carga e raio está localizada na origem do sistema de coordenadas, o cubo vai englobar 1/8 do volume da esfera, logo:
Só que o problema está pedindo o fluxo no na face superior do cubo. Mas, como o campo elétrico é radial, apenas haverá fluxo elétrico na face superior, na face da direita e na face frontal do cubo... as linhas de campo elétrico não atravessarão as faces dos planos , e .
Logo, como o fluxo elétrico passa apenas por 3 faces, o fluxo na face superior do cubo será:
Resposta
Resposta
Ei, a resposta está no passo a passo :)