Energia Potencial e Densidade de Energia, Potencial Elétrico
Duas partículas puntiformes carregadas com a mesma carga positiva, fixas sobre o eixo , estão localizadas simetricamente em relação à origem, uma em e a outra em .
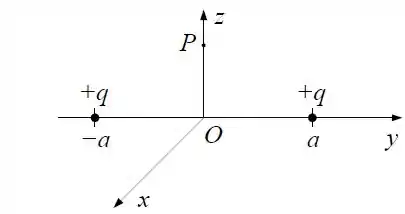
Determine o potencial eletrostático num ponto qualquer do espaço.
Suponha que uma partícula com carga seja abandonada do repouso no ponto com . Determine a energia cinética da carga quando ela passar pela origem do sistema de coordenadas (despreze a forca peso).
Calcule a energia potencial do sistema formado pelas três cargas na configuração em que a carga −Q está no ponto e na configuração em que a carga está na origem . O resultado é compatível com o obtido no item ?
Passo 1
Determine o potencial eletrostático num ponto qualquer do espaço.
O potencial eletrostático de uma carga é dado por:
O potencial eletrostático resultante será a soma dos potenciais de cada carga, portanto:
Onde e são as distâncias da carga o ponto.
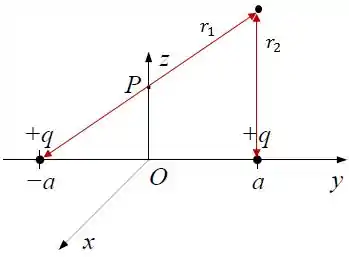
Como as cargas estão localizadas sobre o eixo , a uma distância da origem, podemos escrever e como:
E como as cargas estão dispostas simetricamente, não importa se o ponto estiver à direita ou à esquerda da origem.
Substituindo na expressão de , teremos:
Passo 2
Suponha que uma partícula com carga seja abandonada do repouso no ponto com . Determine a energia cinética da carga quando ela passar pela origem do sistema de coordenadas (despreze a forca peso).
Quando a carga é abandonada do repouso ela possui apenas energia potencial. A partir daí, a carga entra em movimento e a sua energia potencial vai se transformando em energia cinética.
Assim, ao passar pela origem a carga possui energia potencial e energia cinética (que é o queremos descobrir). Logo, supondo que a energia total da carga se conserve:
Passo 3
A energia potencial da carga no ponto é dada por:
A energia potencial da carga no ponto é dada por:
Assim, a energia cinética da carga ao passar pela origem será:
Passo 4
Calcule a energia potencial do sistema formado pelas três cargas na configuração em que a carga −Q está no ponto e na configuração em que a carga está na origem . O resultado é compatível com o obtido no item ?
A energia potencial resultante será a soma das energias potenciais. Beleza?
Temos 3 energias potenciais em casa caso: uma energia potencial entre as cargas e duas energias potenciais entre uma carga e uma carga (porque são duas cargas).
Acontece que nós já calculamos a energia potencial entre a carga e as cargas no ponto e no ponto na letra .
E a energia potencial entre as duas cargas é dada por:
Agora temos apenas que calcular a energia potencial resultante em cada ponto:
Passo 5
Se calcularmos a diferença , veremos que é igual à energia cinética calculada na letra . Logo, o resultado é compatível.
Resposta
O resultado é compatível
Resposta
Ei, a resposta está no passo a passo :)