P2 de Física 3 da USP - 2014
Física 3 - USP
A região entre duas cascas esféricas condutoras concêntricas de raios e com é preenchida com um material de resistividade elétrica , onde é a distância até o centro das cascas esféricas e é uma constante.
Ligando-se uma bateria às cascas esféricas como na figura observa-se uma corrente no sentido indicado.
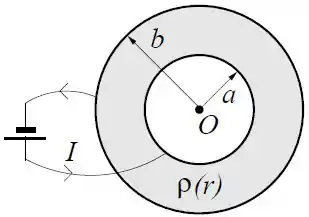
- Calcule o vetor densidade de corrente na região entre as cascas .
- Usando a lei de Ohm, determine o vetor campo elétrico entre as cascas esféricas.
- Calcule a resistência desse sistema em função de , e .
A espira da figura, formada por dois arcos circulares de raio e dois lados retilíneos de comprimento , é percorrida por uma corrente . Um fio retilíneo muito longo transportando uma corrente passa pelo centro de curvatura dos arcos circulares (o fio não está em contato com a espira).
O módulo do campo magnético produzido pelo fio é , onde é a distância ao fio.
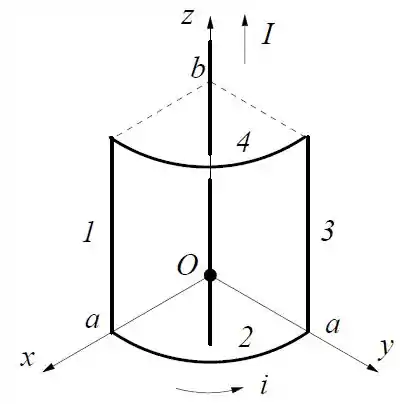
- Calcule o vetor força resultante exercida sobre cada um dos lados da espira pelo fio.
- Calcule o vetor torque resultante em relação à origem exercido sobre a espira pelo fio.
Um circuito no plano formado por uma semicircunferência de raio com centro de curvatura na origem e um trecho reto ao longo do eixo é preenchido por uma corrente no sentido indicado na figura.
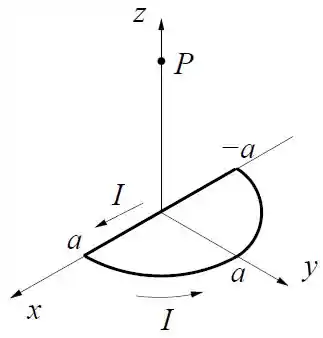
Dado: O elemento de linha infinitesimal de semicircunferência é , onde o ângulo é medido a partir do eixo .
- Calcule o vetor campo magnético produzido pelo trecho reto no ponto .
- Calcule o vetor campo magnético produzido pelo trecho de semicircunferência no ponto .
Um tubo de cobre muito longo de raio interno e raio externo é percorrido por uma corrente uniformemente distribuída “saindo” da página (sentido positivo do eixo ).
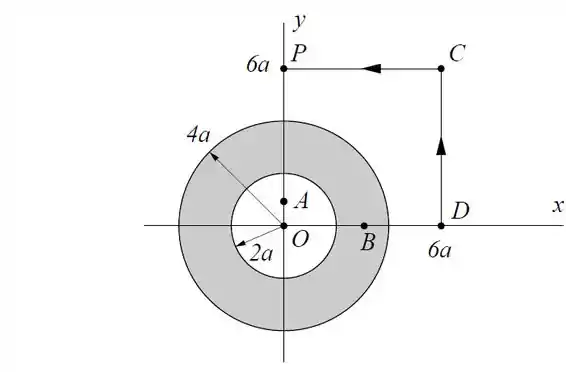
- Determine o vetor campo magnético em coordenadas cartesianas (isto é, na forma ) nos pontos , e .
- Determine a integral de linha do campo magnético ao longo do caminho fechado , onde e , no sentido indicado.
- Determine a integral de linha do campo magnético ao longo do trecho , no sentido indicado.