A espira da figura, formada por dois arcos circulares de raio e dois lados retilíneos de comprimento , é percorrida por uma corrente . Um fio retilíneo muito longo transportando uma corrente passa pelo centro de curvatura dos arcos circulares (o fio não está em contato com a espira).
O módulo do campo magnético produzido pelo fio é , onde é a distância ao fio.
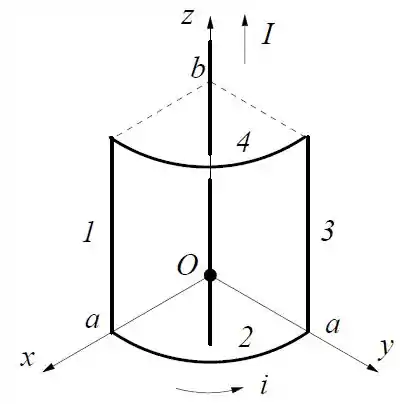
- Calcule o vetor força resultante exercida sobre cada um dos lados da espira pelo fio.
- Calcule o vetor torque resultante em relação à origem exercido sobre a espira pelo fio.
Passo 1
- Calcule o vetor força resultante exercida sobre cada um dos lados da espira pelo fio.
A força magnética sobre um fio que transmite uma corrente é dada por:
Então o segredo aqui é aplicar essa fórmula a cada um dos fios separados...
Antes de analisarmos cada fio, tem um detalhe importante que temos que manter em mente. Pra sabermos a direção e sentido do campo magnético, em cada caso, nós vamos usar a regra da mão direita.
Mas logo de cara, já sabemos que, se o fio central conduz uma corrente no sentido mostrado na figura, o campo magnético terá essa direção:
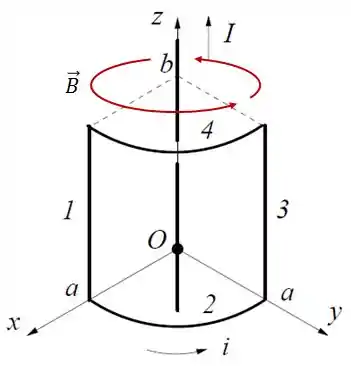
Agora sim, partiu!
Passo 2
- Fio 1:
- Fio 3:
- Fios 2 e 4:
Pro fio 1, o campo magnético nele terá essa cara:
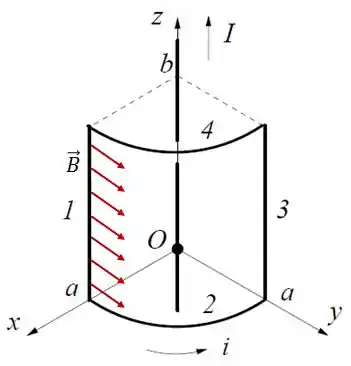
Logo:
Onde , na fórmula que o problema nos deu.
A julgar pelo sentido da corrente, o vetor será:
Integrando dos dois lados:
Logo, a força no fio 1 será:
Eu vou logo para o fio 3 porque a resolução deve ter mais ou menos essa cara.
Passo 3
Agora o campo magnético vai ser algo desse tipo:
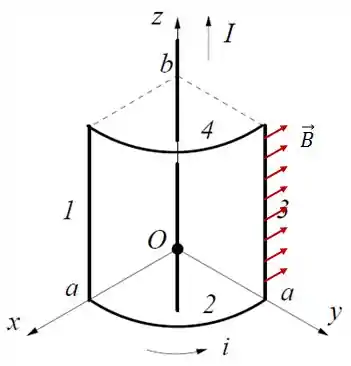
Isso significa que o campo magnético será:
Seguindo o mesmo raciocínio que antes, acompanhando o sentido da corrente :
E a força, por sua vez:
Passo 4
Os dois fios tem uma característica em comum.
No fio 2, o campo magnético vai estar sempre na mesma direção e sentido que , formando um ângulo . No fio 4, o campo magnético vai estar sempre na mesma direção e sentido oposto que , formando um ângulo .
Em ambos os casos:
Logo:
Passo 2
Por definição, o torque é dado por:
Como as forças e estão uniformemente distribuídas ao longo dos fios 1 e 3, os pontos de aplicação dessas forças sobre os fios são os pontos médios desses fios, como mostrado abaixo:
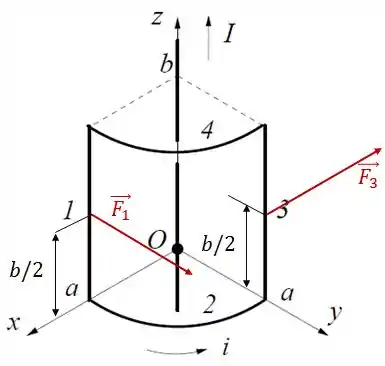
Logo:
Passo 3
O que não podemos esquecer é que o problema pediu o torque resultante, logo: