Um circuito no plano formado por uma semicircunferência de raio com centro de curvatura na origem e um trecho reto ao longo do eixo é preenchido por uma corrente no sentido indicado na figura.
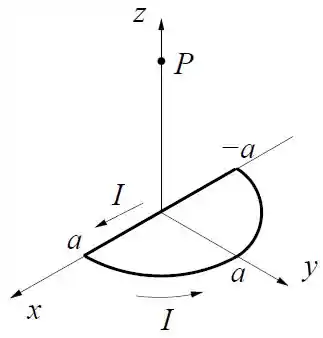
Dado: O elemento de linha infinitesimal de semicircunferência é , onde o ângulo é medido a partir do eixo .
- Calcule o vetor campo magnético produzido pelo trecho reto no ponto .
- Calcule o vetor campo magnético produzido pelo trecho de semicircunferência no ponto .
Passo 1
- Calcule o vetor campo magnético produzido pelo trecho reto no ponto .
- Calcule o vetor campo magnético produzido pelo trecho de semicircunferência no ponto .
Aqui não tem muito erro, nesse tipo de problema, a primeira coisa que vem à cabeça é... isso, isso mesmo, Biot-Savart:
Só que podemos escrever esse vetor unitário da seguinte forma:
Logo:
Agora só temos que definir quem é e .
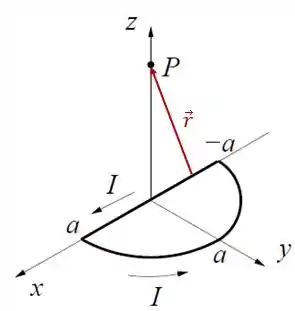
Para o é importante sempre seguir o sentido da corrente, logo:
Olhando a figura aqui em cima, podemos escrever como:
Logo:
Agora é só voltar para a lei de Biot-Savart e ser feliz.
Passo 2
Se você nunca fez essa integral antes, ela parece ser escrota. Você deve imaginar isso porque, na verdade, ela é escrota mesmo.
Não é uma boa quebrarmos a cabeça com ela e fazer esse troço ficar gigante, até porque ela provavelmente vai ser dada no formulário da prova, caso você tenha que resolvê-la. Mas, na dúvida, eu vou te dar o caminho certo pra resolver essa integral, tranquilo?
Ela é resolvida fazendo uma substituição trigonométrica, chamando , e . Faz isso, e resolve a integral, a única coisa que você precisa saber além disso é que .
Bom, o que você vai encontrar é isso aqui:
Passo 3
O esquema aqui é um pouco diferente de antes, mas não de preocupa se começar a parecer feio, ok?
Vamos começar definindo quem é e .
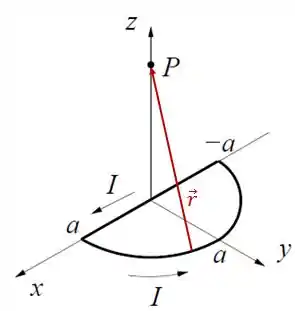
Portando:
Agora podemos voltar para Biot-Savart:
Sim, ficou feio, ficou escroto... mas tá certo!