Um tubo de cobre muito longo de raio interno e raio externo é percorrido por uma corrente uniformemente distribuída “saindo” da página (sentido positivo do eixo ).
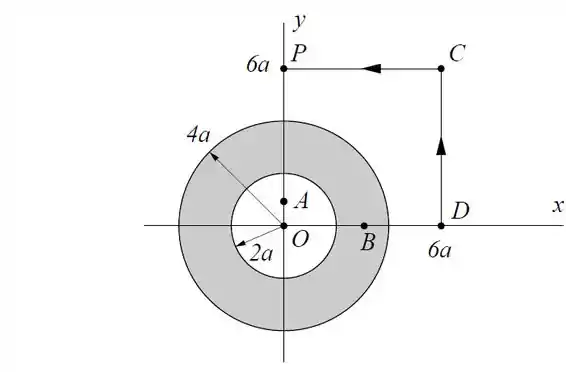
- Determine o vetor campo magnético em coordenadas cartesianas (isto é, na forma ) nos pontos , e .
- Determine a integral de linha do campo magnético ao longo do caminho fechado , onde e , no sentido indicado.
- Determine a integral de linha do campo magnético ao longo do trecho , no sentido indicado.
Passo 1
- Determine o vetor campo magnético em coordenadas cartesianas (isto é, na forma ) nos pontos , e .
Sim, é isso mesmo que você tá pensando... lei de Ampère!
Aqui não tem muito erro, é aplicar a lei de Ampère e ser feliz.
Vamos começar pelo ponto .
Passo 2
Vamos imaginar então uma circunferência de raio para calcular o campo magnético.
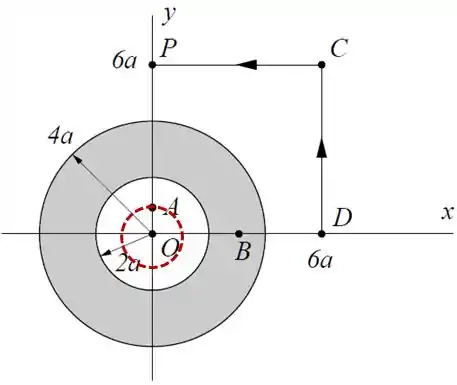
Dentro da nossa curva:
Logo, .
Passo 3
O esquema agora é o mesmo de antes, vamos imaginar uma circunferência de raio .
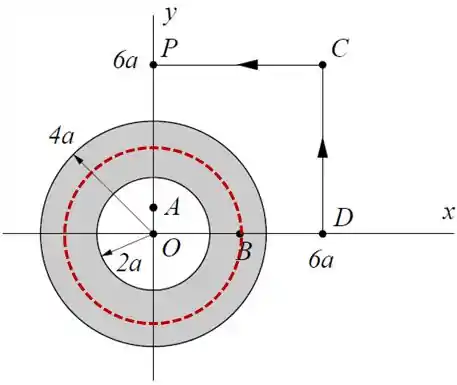
Pra determinar a corrente , basta usar uma regra de três simples:
Substituindo na lei de Ampère:
Se a corrente está “saindo” da página, usando a regra da mão direita, vemos que o vetor campo magnético será:
Passo 4
Nesse ponto, , e o campo magnético terá o seguinte sentido:
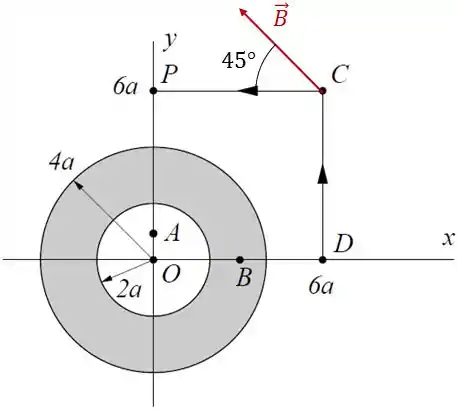
Portanto, de acordo com a lei de Ampère:
Passo 2
O problema está pedindo para calcularmos:
Mas, de acordo com a lei de Ampère:
E a corrente nesse caso vale , logo:
Passo 3
Nas retas, e , o campo magnético é perpendicular:
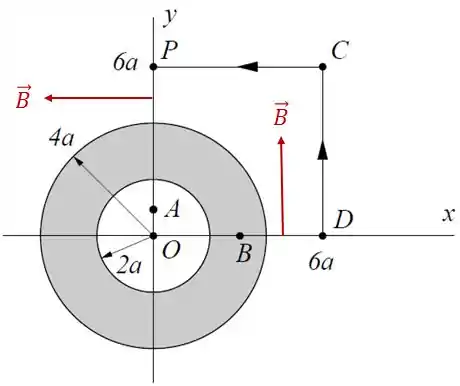
Isso significa que esses trechos não contribuem na integral, pois como é perpendicular a , o produto escalar . Logo:
Resposta
-
Ponto :
Ponto :
Ponto :