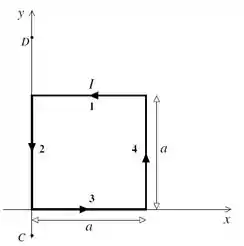
Uma corrente estacionária circula no sentido anti-horário de uma espira condutora quadrada, de lado . A figura ao lado mostra a espira em um sistema de coordenadas tal que o plano da espira coincide com o plano . Considere o campo magnético (no mesmo sistema de coordenadas)
- Calcule as forças magnéticas que atuam em cada um dos lados da espira (como indicados na figura). Calcule também a força resultante sobre a espira.
- Suponha que o movimento da espira seja restrito a rotações em torno de um eixo vertical fixo passando pelos pontos (veja a figura). Calcule o torque em torno deste eixo em relação à origem.
Sugestão para os itens e Calcule primeiramente as forças infinitesimais e em seguida obtenha , efetuando a integral correspondente.
Passo 1
a)Primeiro, vamos calcular o campo magnético em cada lado da espira:
As forças magnéticas a gente calcula usando a equação
Sendo que e .
Para e , o produto vetorial na equação acima resulta em , portanto
Agora vamos calcular e substituindo os valores de e na equação
Para :
Integrando de até :
Agora para :
Integrando de até :
Agora temos , , e , mas o enunciado nos pede também a força resultante . Ela vai ser dada por:
Passo 2
b)O torque só vai ser calculado pra e vai ser zero, já que essas forças são nulas ok?
A força infinitesimal atua sobre um elemento de comprimento . O seu torque infinitesimal será dado por
Integrando de até :
Já para , como essa força atua sobre o eixo de rotação , o torque será nulo.