A figura abaixo mostra trechos de um fio condutor reto e uma fita condutora de comprimentos e , respectivamente. A fita possui largura e sua espessura pode ser desconsiderada. Correntes e percorrem o fio e a fita, respectivamente. A densidade linear de corrente na fita é uniforme .
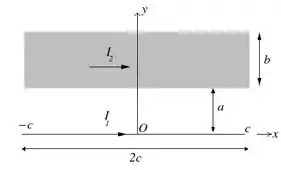
- Usando a Lei de Biot-Savart, calcule o vetor campo magnético produzido pelo fio num ponto situado ao longo do eixo .
- Considerando que agora o fio é infinito, , e a fita é infinita ao longo da direção , calcule o vetor força por unidade de comprimento produzida pelo fio sobre a fita.
Passo 1
a) A lei de Biot-Savart fala pra gente que o elemento do fio transportando uma corrente produz um campo magnético infinitesimal ao longo do eixo , esse campo é escrito como:
Agora a gente pode fazer o produto vetorial e integrar a equação acima entre e pra sair desse elemento infinitesimal, assim vamos chegar em
Passo 2
b)Se calcularmos o limite de com , a expressão para vai ser escrita como
Ok, agora precisamos calcular a força magnética que é produzida na fita, ela vai ser escrita como
Substituindo o campo pelo calculado e a nossa densidade de corrente por
Agora só precisamos integrar a expressão acima de até .
Como o enunciado nos pede a força por unidade de comprimento , vamos passar o pro outro lado dividindo, chegando no nosso resultado: