Um fio condutor muito longo e de seção cilíndrica de raio está envolto por uma casca
cilíndrica de raio , formando um cabo coaxial. No fio há uma densidade de corrente
uniforme e na casca uma densidade de corrente superficial , sendo
e constantes positivas. Expresse suas respostas em termos dos parâmetros
dados:
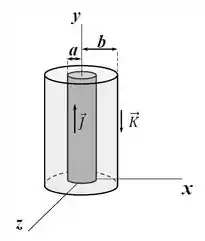
- Calcule o campo magnético nos pontos onde ( é a distância do ponto até o eixo ).
- Calcule o campo magnético na região exterior da casca cilíndrica ().
- Determine o valor de tal que o campo seja nulo na região .
Passo 1
Antes de tudo, temos que perceber que como a corrente percorre no eixo , pela regra da mão direita, as linhas de campo magnético vão formar circunferências concêntricas, e não vamos esquecer que o vetor aponta tangencialmente em cada ponto da linha (vamos especificar como o versor .
Para calcularmos o campo magnético, vamos utilizar a lei de Ampére:
Como o campo magnético forma circunferências concêntricas, a gente pode escrever a equação assim:
A corrente é distribuída uniformemente entre e , então a corrente englobada é escrita como
Lembrando: é a distância entre a linha amperiana e o eixo .
Passo 2
a)Para calcularmos o campo magnético com entre e , precisamos da nossa corrente . Nesse caso, ela vai ser toda a corrente englobada entre e :
Então, o campo magnético nesse caso vai ser
Passo 3
b)No caso de , a corrente englobada vai ser
Então o nosso campo magnético vai ser
Passo 4
c)Para encontrar quando o campo magnético vai ser nulo, vamos igualar a 0 a expressão do passo 2 (campo magnético para ) e então isolamos