P3 de Física 3 da USP - 2015

Um anel condutor de raio está no plano e centrado na origem de um sistema de coordenadas. Outro anel condutor , concêntrico a possui raio , conforme a figura.

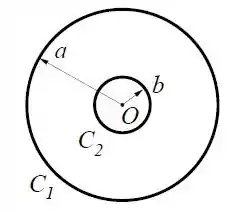
Calcule a indutância mútua entra os dois anéis. Justifique as aproximações feitas.

No anel circula uma corrente . Calcule a força eletromotriz induzida no anel 1 pelo anel 2.

Dado: O campo magnético no centro de um anel de raio por onde passa uma corrente é .

Uma barra condutora é movida com velocidade constante , sobre dois fios condutores separados por uma distância . A coordenada da barra no instante é .

Um resistor de resistência em está conectado às extremidades dos dois fios, formando o circuito fechado mostrado na figura. Um campo magnético uniforme e crescente com o tempo , onde , está presente na região. Nas perguntas abaixo considere o tempo apenas no intervalo .

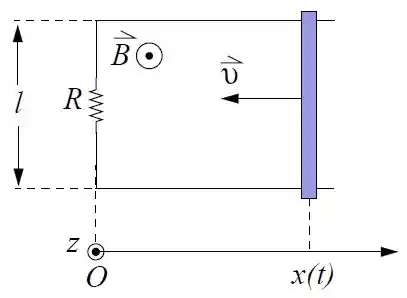
Determine a força eletromotriz induzida no circuito como função do tempo .

Calcule a corrente induzida no circuito e determine o instante de tempo no qual ela se anula.

Determine o sentido da corrente (horário ou anti-horário) como função do tempo .

Uma onda eletromagnética plana senoidal polarizada na direção do eixo propaga-se no vácuo na direção dos valores crescentes do eixo . A frequência da onda é e o valor máximo atingido pela componente magnética da onda é na origem do sistema de coordenadas no instante .

Escreva as expressões dos vetores campo elétrico e campo magnético da onda como função do tempo e posição. Todos os parâmetros da expressão devem ser numéricos.

Determine o vetor de Poynting da onda. Todos os parâmetros da expressão devem ser numéricos.

Considere agora a incidência desta onda sobre uma placa totalmente absorvedora de área , que se encontra em uma posição paralela ao plano em . Calcule a energia absorvida pela placa após um intervalo de tempo de incidência igual a três vezes o período da onda. A resposta deve ser numérica.

O campo elétrico na região considerada na figura é dado por sendo uma constante positiva.

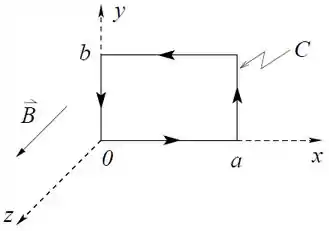
Calcule a densidade de carga na região.

O campo elétrico na região considerada na figura é dado por sendo uma constante positiva.

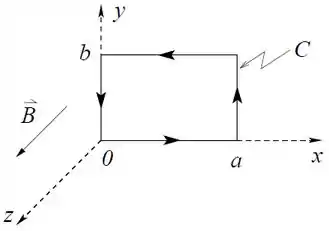
Calcule a integral de linha ao longo do retângulo de largura e altura , orientado como é mostrado na figura.

Além do campo elétrico na região considerada há também um campo magnético uniforme cuja intensidade depende do tempo. Em , . Utilizando a Lei de Faraday na forma integral, determine .