Uma barra condutora é movida com velocidade constante , sobre dois fios condutores separados por uma distância . A coordenada da barra no instante é .
Um resistor de resistência em está conectado às extremidades dos dois fios, formando o circuito fechado mostrado na figura. Um campo magnético uniforme e crescente com o tempo , onde , está presente na região. Nas perguntas abaixo considere o tempo apenas no intervalo .
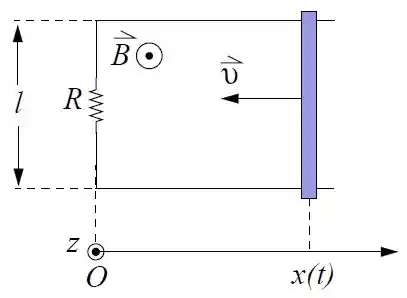
Determine a força eletromotriz induzida no circuito como função do tempo .
Calcule a corrente induzida no circuito e determine o instante de tempo no qual ela se anula.
Determine o sentido da corrente (horário ou anti-horário) como função do tempo .
Passo 1
Determine a força eletromotriz induzida no circuito como função do tempo .
Opa! Quando o cara fala de fem induzida, nós já temos que pensar logo em Lei de Faraday, que é dada por:
O fluxo magnético é dado por:
Como o campo magnético é uniforme (ou seja, não varia com o espaço):
Onde
Voltando para a Lei de Faraday:
Como a barra sai de uma posição inicial e vai se movendo da direita para a esquerda, podemos reescrever como:
Além disso, o próprio problema já nos disse que o módulo do campo magnético é dado por . Logo, substituindo esses caras na Lei de Faraday:
Agora é só dar uma arrumada nesse cara:
Passo 2
Calcule a corrente induzida no circuito e determine o instante de tempo no qual ela se anula.
Ah! Agora que já calculamos a fem induzida, calcular a corrente induzida é tranquilo. Basta usar a Lei de Ohm.
Substituindo aqui o que encontramos na letra :
Essa corrente vai se anular quando:
Passo 3
Determine o sentido da corrente (horário ou anti-horário) como função do tempo .
A expressão que encontramos na Lei de Faraday foi a seguinte:
Na letra , vimos que a corrente se anula quando .
Então temos dois intervalos distintos aqui...
Nesse intervalo, tanto quanto são negativos, isso significa que a corrente estará no sentido horário.
Nesse intervalo, tanto quanto são positivos, isso significa que a corrente estará no sentido anti-horário.
Resposta
: Corrente no sentido horário;
: Corrente no sentido anti-horário.