O campo elétrico na região considerada na figura é dado por sendo uma constante positiva.
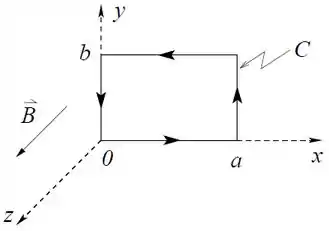
Calcule a integral de linha ao longo do retângulo de largura e altura , orientado como é mostrado na figura.
Além do campo elétrico na região considerada há também um campo magnético uniforme cuja intensidade depende do tempo. Em , . Utilizando a Lei de Faraday na forma integral, determine .
Passo 1
Calcule a integral de linha ao longo do retângulo de largura e altura , orientado como é mostrado na figura.
O campo elétrico é dado por:
Pra analisar corretamente, vamos dividir a o retângulo em 4 retas.
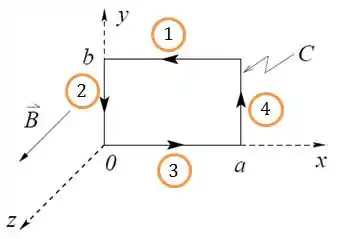
- Retas 2 e 4
- Reta 3
- Reta 1
Nas retas 2 e 4, o vetor é, respectivamente:
Assim, nesses dois casos, o produz escalar é nulo.
Na reta 3, . Portanto .
Nesse caso, o campo elétrico é dado por:
E o vetor é dado por:
Portanto:
Passo 2
Além do campo elétrico na região considerada há também um campo magnético uniforme cuja intensidade depende do tempo. Em , . Utilizando a Lei de Faraday na forma integral, determine .
A lei de Faraday é dada por:
Na forma integral, podemos reescrever a fem como:
Portanto:
Essa integral nós já calculamos na letra , e como a área é constante, o fluxo magnético vai variar apenas de acordo com .
Onde . Logo:
Simplificando essa expressão:
De acordo com o problema o campo magnético é crescente e tem um valor inicial , logo, integrando esse cara:
Resposta