PREC de Física 3 da USP - 2014

A figura abaixo mostra uma seção transversal de dois fios condutores longos, idênticos, com comprimento , estendidos paralelamente um ao lado do outro ao longo da direção . Por estes fios circulam correntes e , em sentidos opostos, sendo no mesmo sentido do eixo , conforme a figura.

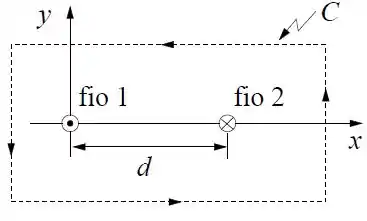
Usando a lei de Ampère, calcule o vetor campo magnético de um fio infinito onde passa uma corrente .

Calcule a força de interação por unidade de comprimento que o fio 1 exerce sobre o fio 2. A força é atrativa ou repulsiva?

Calcule a integral sobre o percurso orientado no sentido anti-horário, conforme a figura.

Um bastão de comprimento , eletrizado com densidade de carga não uniforme está disposto ao longo do eixo .

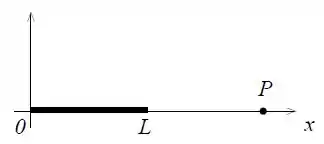
Determine o potencial eletrostático devido ao bastão para um ponto sobre o eixo com coordenada . Adote o potencial nulo no infinito.

Determine o vetor força de interação eletrostática sobre uma carga pontual em .

No circuito abaixo, com o capacitor descarregando, a corrente atinge o seu valor máximo no instante .

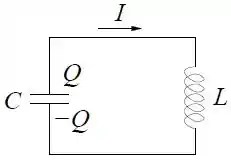
Escreva a equação diferencial para a carga na placa superior do capacitor. Usando o fato de que a corrente é máxima no instante , demostre que .

Escreva a solução geral da equação. Determine a carga e a corrente no circuito para satisfazendo as condições iniciais e .

Calcule a energia total no circuito e mostre que ela se conserva.

A figura ao lado mostra a seção transversal de uma região cilíndrica de raio , coaxial com o eixo de um sistema de coordenadas, onde existe um campo magnético uniforme dado por

constante

de modo que e .

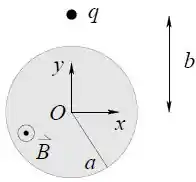
Obtenha o vetor campo elétrico induzido em todo o espaço, em função de , e .

A figura também mostra uma partícula com carga . Para a partícula na posição indicada na figura , obtenha o vetor força elétrica que atua sobre ela. Calcule também o vetor torque da força elétrica em relação à origem do sistema de coordenadas. Expresse os vetores sob a forma cartesiana, isto é, em termos das componentes nas direções , e .