Força e Torque sobre uma Espira, Lei de Ampère
A figura abaixo mostra uma seção transversal de dois fios condutores longos, idênticos, com comprimento , estendidos paralelamente um ao lado do outro ao longo da direção . Por estes fios circulam correntes e , em sentidos opostos, sendo no mesmo sentido do eixo , conforme a figura.
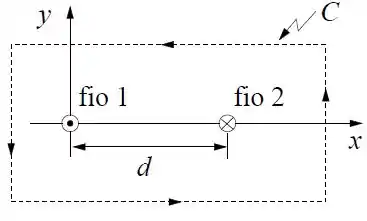
Usando a lei de Ampère, calcule o vetor campo magnético de um fio infinito onde passa uma corrente .
Calcule a força de interação por unidade de comprimento que o fio 1 exerce sobre o fio 2. A força é atrativa ou repulsiva?
Calcule a integral sobre o percurso orientado no sentido anti-horário, conforme a figura.
Passo 1
Usando a lei de Ampère, calcule o vetor campo magnético de um fio infinito onde passa uma corrente .
Esse é um problema clássico de lei de Ampère, que é dada por:
Para o caso de um fio infinito, vamos usar uma amperiana de formado circular, centrada com o fio.
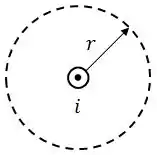
Para esse caso, podemos simplificar a lei de Ampère para:
Onde é a corrente envolvida pela amperiana.
Logo:
A direção e sentido do vetor campo magnético são determinados pela regra da mão direita.
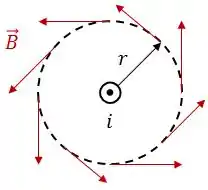
Passo 2
Calcule a força de interação por unidade de comprimento que o fio 1 exerce sobre o fio 2. A força é atrativa ou repulsiva?
A força magnética sobre um fio retilíneo é dado por:
Onde o vetor tem a mesma direção e sentido da corrente.
Assim, a força que o fio 1 exerce sobre o fio 2 será:
Sobre o fio 2, o campo magnético gerado pelo fio 1 será:
Além disso, . Portanto:
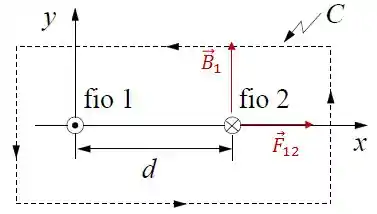
A partir da imagem acima, podemos concluir que a força é repulsiva.
O último detalhe importante do problema é que ele pede a força por unidade de comprimento. Assim, para ficar tudo perfeito, só nos resta fazer:
Passo 3
Calcule a integral sobre o percurso orientado no sentido anti-horário, conforme a figura.
Se olharmos novamente pra lei de Ampère:
Podemos ver que calcular a integral vai ser uma tarefa mais fácil do que parece.
A partir da lei de Ampère, a única coisa que temos que fazer aqui é calcular a corrente interna .
Como o problema disse que o percurso está orientado no sentido anti-horário, de acordo com a regra da mão direita, vamos considerar as correntes que estão entrando no plano da página como negativas e as correntes que estão saindo do plano da página, como positivas.
Logo:
Portanto:
Resposta
A força é repulsiva