Capacitores e Dielétricos, Indutância
No circuito abaixo, com o capacitor descarregando, a corrente atinge o seu valor máximo no instante .
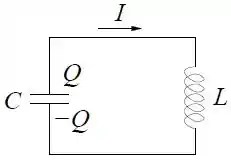
Escreva a equação diferencial para a carga na placa superior do capacitor. Usando o fato de que a corrente é máxima no instante , demostre que .
Escreva a solução geral da equação. Determine a carga e a corrente no circuito para satisfazendo as condições iniciais e .
Calcule a energia total no circuito e mostre que ela se conserva.
Passo 1
Escreva a equação diferencial para a carga na placa superior do capacitor. Usando o fato de que a corrente é máxima no instante , demostre que .
Usando a lei das malhas, a somas das diferenças de potencial entre todos os elementos do circuito deve ser nulo, logo:
Sabendo que, durante a descarga do capacitor, , teremos:
Dividindo todos os termos por , teremos:
Passo 2
Para demonstrar que , vamos voltar à equação inicial:
O problema disse que, em , a corrente é máxima, logo:
Sendo assim:
Passo 3
Escreva a solução geral da equação. Determine a carga e a corrente no circuito para satisfazendo as condições iniciais e .
A equação diferencial de que encontramos na letra foi:
A solução geral da equação diferencial acima é:
Onde:
Passo 4
A partir daqui, vamos usar as condições iniciais do problema pra encontrar os valores de e , ok?
A partir dessas condições, teremos:
Finalmente, substituindo as constantes, teremos:
Passo 5
Calcule a energia total no circuito e mostre que ela se conserva.
A energia total do sistema será a soma das energias do capacitor e do indutor, logo:
Substituindo as expressões de e , teremos:
Lembrando que:
Teremos:
Sabendo que , finalmente, teremos:
Portanto, a energia do circuito é constante, provando que ela se conserva, independente do estado do circuito.
Resposta