A figura ao lado mostra a seção transversal de uma região cilíndrica de raio , coaxial com o eixo de um sistema de coordenadas, onde existe um campo magnético uniforme dado por
constante
de modo que e .
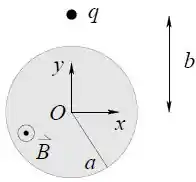
Obtenha o vetor campo elétrico induzido em todo o espaço, em função de , e .
A figura também mostra uma partícula com carga . Para a partícula na posição indicada na figura , obtenha o vetor força elétrica que atua sobre ela. Calcule também o vetor torque da força elétrica em relação à origem do sistema de coordenadas. Expresse os vetores sob a forma cartesiana, isto é, em termos das componentes nas direções , e .
Passo 1
Obtenha o vetor campo elétrico induzido em todo o espaço, em função de , e .
Aqui vai ser necessário interligarmos alguns conhecimentos que temos sobre a matéria, beleza?
Bom, mesmo que a área transversal da região permaneça constante, a variação do campo magnético com o tempo vai gerar uma variação do fluxo magnético com o tempo, concorda?
De acordo com a lei de Faraday, a variação desse fluxo magnético vai gerar uma induzida, dada por:
Onde , logo:
Até aqui, tudo bem?
Agora é importante lembrar que nós podemos associar a induzida com o campo elétrico induzido através da relação:
Substituindo isso na lei de Faraday, teremos:
Agora sim, podemos seguir em frente.
Passo 2
Por conta da simetria do problema, , onde é tangencial à circunferência de raio e positivo no sentido anti-horário.
Como temos que determinar o campo elétrico em toda a região do espaço, vamos dividir o espaço em 2: e , ok?
Nesse caso, devemos considerar o fluxo magnético apenas sobre a região de raio :
Finalmente:
Aqui vamos considerar o fluxo magnético sobre toda a região de raio :
Finalmente:
Passo 3
A figura também mostra uma partícula com carga . Para a partícula na posição indicada na figura , obtenha o vetor força elétrica que atua sobre ela. Calcule também o vetor torque da força elétrica em relação à origem do sistema de coordenadas. Expresse os vetores sob a forma cartesiana, isto é, em termos das componentes nas direções , e .
Por definição, a força elétrica e o campo elétrico estão associados por:
No ponto onde está a carga o campo elétrico terá a direção e sentido do vetor .
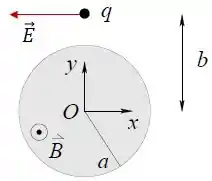
Logo:
Finalmente:
Passo 4
O torque, por definição é dado por:
Logo:
Resposta
Resposta
Ei, a resposta está no passo a passo :)