PREC de Física 3 da USP - 2015

Em um condutor cilíndrico muito longo, maciço, de raio passa uma corrente cuja densidade varia linearmente com a distancia ao eixo do cilindro segundo a expressão , onde é uma constante.

Calcule a corrente através do disco de raio mostrado na figura.

Calcule o vetor para .

Calcule o vetor para .

O anel de resistência elétrica , contido no plano , é constituído por um condutor elástico, o que possibilita variações de seu raio .

Durante o intervalo de tempo o raio do anel diminui segundo a equação , onde é constante. O campo magnético presente na região é uniforme e ortogonal ao plano .

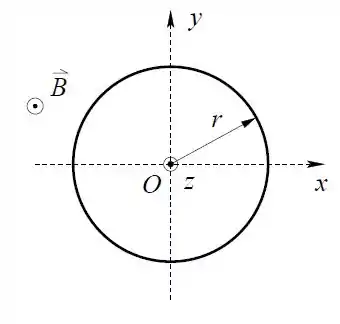
Nas perguntas abaixo considere o tempo apenas no intervalo .

Determine a força eletromotriz induzida no anel em função de .

Calcule a corrente induzida no anel e determine o seu sentido (horário ou anti-horário).

Calcule o campo magnético produzido pela corrente induzida no centro do anel. Se você não resolveu o item deixe sua resposta em função da corrente induzida .

Uma camada esférica condutora, com carga , tem raio interno e raio externo . No centro da camada, na cavidade interna, há uma carga puntiforme , conforme a figura.

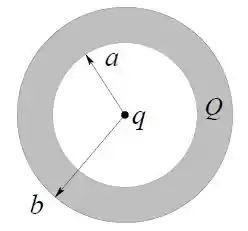
Usando a lei de Gauss e propriedades dos condutores em equilíbrio eletrostático calcule o vetor campo elétrico em todo o espaço.

A partir do campo elétrico calcule o potencial elétrico na região 1 , na região 2 e na região 3 . Defina o potencial no infinito igual a zero.

Uma onda eletromagnética plana monocromática que se propaga no vácuo possui um campo elétrico descrito pela expressão onde e são constantes positivas.

Determina a direção e o sentido de propagação da onda. Calcule o comprimento de onda e a frequência da onda em função das constantes e .

Qual relação deve haver entre e para que satisfaça a equação de onda da luz se propagando no vácuo?

Determine o vetor em função de , , e da velocidade da luz no vácuo .

Calcule o vetor de Poynting instantâneo e a densidade de energia média desta onda.