Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Carga Pontual

Ver Teoria
Exercício 961234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495979899100

Enunciado

Lei de Gauss, Campo em Condutores, Potencial Elétrico

Uma camada esférica condutora, com carga Q > 0 , tem raio interno a e raio externo b . No centro da camada, na cavidade interna, há uma carga puntiforme q > 0 , conforme a figura.

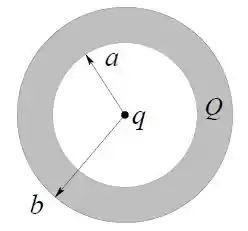
a ) Usando a lei de Gauss e propriedades dos condutores em equilíbrio eletrostático calcule o vetor campo elétrico em todo o espaço.

b ) A partir do campo elétrico calcule o potencial elétrico na região 1 r ≥ b , na região 2 a ≤ r ≤ b e na região 3 0 ≤ r ≤ a . Defina o potencial no infinito igual a zero.

Passo 1

a ) Usando a lei de Gauss e propriedades dos condutores em equilíbrio eletrostático calcule o vetor campo elétrico em todo o espaço.

A lei de Gauss é dada por:

∯ G   E → ∙ d A → = Q i n t ϵ 0

Como o problema tem geometria esférica, podemos simplificar a lei de Gauss para:

E A = Q i n t ϵ 0

E 4 π r 2 = Q i n t ϵ 0

E = Q i n t 4 π ϵ 0 r 2

Novamente aproveitando a simetria esférica do problema, o vetor campo elétrico terá direção radial, logo:

E → = Q i n t 4 π ϵ 0 r 2 r ^

Agora, o nosso único trabalho é, para cada região, calcular a carga interna à gaussiana de raio r .

Passo 2

-
  • Região 1 r ≥ b

    • Essa região engloba tanto a casca esférica quanto a carga pontual, logo:

    Q i n t = Q + q

    Finalmente:

    E → = 1 4 π ϵ 0 Q + q r 2 r ^

  • Região 2 a ≤ r ≤ b

    • Essa região corresponde à região no interior do condutor, certo?

    Então aqui vai uma coisa que você precisa guardar nesse coração... o campo elétrico no interior de um condutor é SEMPRE igual a zero.

    Então ficou fácil para nós:

    E → = 0 →

  • Região 3 0 ≤ r ≤ a

    • Essa região engloba somente a carga pontual, sendo assim:

    Q i n t = q

    Portanto:

    E → = 1 4 π ϵ 0 q r 2 r ^

    Passo 3

    b ) A partir do campo elétrico calcule o potencial elétrico na região 1 r ≥ b , na região 2 a ≤ r ≤ b e na região 3 0 ≤ r ≤ a . Defina o potencial no infinito igual a zero.

    O potencial elétrico está associado ao campo elétrico através da expressão:

    V B - V A = - ∫ A B E → ∙ d l →

    V B - V A = - ∫ r A r B E r d r

    Então só precisamos fazer esse cálculo para cada situação.

    Passo 4

  • Região 1 r ≥ b

    • Conforme calculamos no item a , nessa região, o campo elétrico é dado por:

    E → = 1 4 π ϵ 0 Q + q r 2 r ^

    Logo:

    V 1 r - V ∞ = - ∫ ∞ r 1 4 π ϵ 0 Q + q r 2 d r

    De acordo com o problema, V ∞ = 0 , logo:

    V 1 r - 0 = 1 4 π ϵ 0 Q + q r ∞ r    

    V 1 r = 1 4 π ϵ 0 Q + q r    

  • Região 2 a ≤ r ≤ b

    • De acordo com o que encontramos anteriormente:

    E → = 0 →

    Logo:

    V 2 r - V 2 b = - ∫ b r 0   d r = 0

    V 2 r = V 2 b

    Como o potencial é uma função contínua, V 2 b = V 1 b . Portanto:

    V 2 r = V 1 b

    V 2 r = 1 4 π ϵ 0 Q + q b

    Assim, o potencial nessa região é constante.

  • Região 3 0 ≤ r ≤ a

    • Nessa região:

    E → = 1 4 π ϵ 0 q r 2 r ^

    Assim, o potencial elétrico será dado por:

    V 3 r - V 3 a = - ∫ a r 1 4 π ϵ 0 q r 2   d r

    Novamente, como o potencial é uma função contínua:

    V 3 a = V 2 a = 1 4 π ϵ 0 Q + q b

    Voltando aos cálculos, teremos:

    V 3 r - 1 4 π ϵ 0 Q + q b = - ∫ a r 1 4 π ϵ 0 q r 2   d r

    V 3 r - 1 4 π ϵ 0 Q + q b = 1 4 π ϵ 0 q r a r

    V 3 r - 1 4 π ϵ 0 Q + q b = 1 4 π ϵ 0 q r - 1 4 π ϵ 0 q a

    Organizando esse cara, teremos:

    V 3 r = 1 4 π ϵ 0 q r - 1 4 π ϵ 0 q a + 1 4 π ϵ 0 Q + q b

    Resposta

    a )

  • Região 1 r ≥ b

    • E → = 1 4 π ϵ 0 Q + q r 2 r ^

  • Região 2 a ≤ r ≤ b

    • E → = 0 →

  • Região 3 0 ≤ r ≤ a

    • E → = 1 4 π ϵ 0 q r 2 r ^

    b )

  • Região 1 r ≥ b

    • V 1 r = 1 4 π ϵ 0 Q + q r    

  • Região 2 a ≤ r ≤ b

    • V 2 r = 1 4 π ϵ 0 Q + q b

  • Região 3 0 ≤ r ≤ a

V 3 r = 1 4 π ϵ 0 q r - 1 4 π ϵ 0 q a + 1 4 π ϵ 0 Q + q b

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Considere uma carga pontual q = 1,0 μC, o ponto A a uma distância d 1 = 2,0m de q e o ponto B a uma distância d 2 = 1,0m de q. (a) Se A e B estão diametralmente opostos, como na figura da esquerda aba
A figura (a) mostra duas partículas carregadas. A partícula 1, de carga q 1 , é mantida fixa no lugar a uma distância d da origem. A partícula 2, de carga q 2 , pode ser deslocada ao longo do eixo x.
Na figura (a), uma partícula de carga +e está inicialmente no ponto z = 20 nm do eixo de um dipolo elétrico, do lado positivo do dipolo. (A origem do eixo zé o centro do dipolo.) A partícula é desloca
A figura (a) mostra três partículas no eixo x. A partícula 1 (com uma carga de +5,0 μC) e a partícula 2 (com uma carga de +3,0 μC) são mantidas fixas no lugar, separadas por uma distância d = 4,0 cm.
Um pósitron (carga + e , massa igual à do elétron) está se movendo com uma velocidade de 1 , 0 · 10 7m / s no sentido positivo do eixo x quando, em x = 0 , encontra um campo elétrico paralelo ao eixo