O anel de resistência elétrica , contido no plano , é constituído por um condutor elástico, o que possibilita variações de seu raio .
Durante o intervalo de tempo o raio do anel diminui segundo a equação , onde é constante. O campo magnético presente na região é uniforme e ortogonal ao plano .
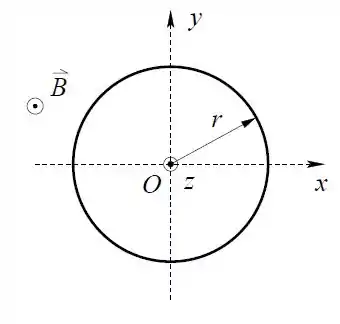
Nas perguntas abaixo considere o tempo apenas no intervalo .
Determine a força eletromotriz induzida no anel em função de .
Calcule a corrente induzida no anel e determine o seu sentido (horário ou anti-horário).
Calcule o campo magnético produzido pela corrente induzida no centro do anel. Se você não resolveu o item deixe sua resposta em função da corrente induzida .
Passo 1
Determine a força eletromotriz induzida no anel em função de .
A força eletromotriz induzida no anel é dada pela lei de Faraday:
Onde o fluxo magnético é dado por:
Substituindo a expressão de dada pelo problema, teremos:
Voltando para a expressão de , teremos:
Passo 2
Calcule a corrente induzida no anel e determine o seu sentido (horário ou anti-horário).
Agora que já calculamos a induzida, a nossa vida ficou um pouco mais fácil.
Passo 3
O sentido da corrente é determinado pela lei de Lenz, que diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
É o seguinte... se o fluxo magnético está aumentando, a corrente induzida gerará um campo magnético no sentido contrário ao fluxo (nesse caso, a corrente estaria no sentido horário), querendo “atrapalhar” o fluxo.
Se o fluxo magnético está diminuindo, a corrente induzida gerará um campo magnético no mesmo sentido do fluxo (nesse caso, a corrente estaria no sentido anti-horário), querendo “ajudar” o fluxo.
Aqui, como o campo magnético é uniforme e constante e o raio está diminuindo com o tempo (logo, a área também está diminuindo), o fluxo magnético está diminuindo, logo, a corrente induzida está no sentido anti-horário.
Passo 4
Calcule o campo magnético produzido pela corrente induzida no centro do anel. Se você não resolveu o item deixe sua resposta em função da corrente induzida .
Podemos calcular o campo magnético através da lei de Biot-Savart, dada por:
Onde os vetores e estão representados abaixo:
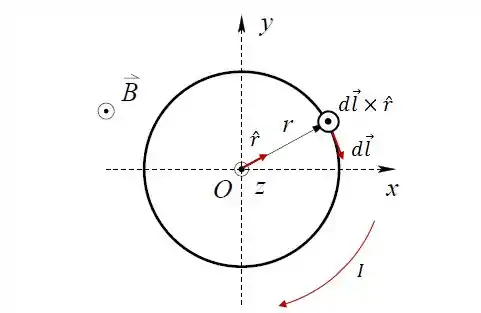
Daqui podemos tirar que .
Logo, substituindo na expressão de , teremos:
Pra finalizar, temos apenas que substituir a expressão que encontramos para .
Como , teremos:
Resposta
A corrente induzida está no sentido anti-horário.