Seja a colisão entre uma esfera de massa , cujo vetor posição é dado por e outra esfera de massa e vetor posição é dado por Imediatamente após a colisão, a esfera adquire uma velocidade de módulo e faz um ângulo de em relação ao eixo positivo. Considere o sistema isolado. Justifique suas respostas.
(a) Dado que o momento total do sistema imediatamente antes da colisão é , determine a velocidade do centro de massa imediatamente após a colisão.
(b) Determine a velocidade da esfera A imediatamente após a colisão.
(c) Determine se a colisão foi elástica ou inelástica.
Passo 1
(a)Conservação do momento linear para o centro de massa
Prestou bastante atenção no enunciado? Nada de forças externas atuando, não é mesmo? Então podemos trabalhar com a conservação do momento linear pro centro de massa do sistema de partículas. Dá uma olhada:
Vamos considerar como “inicial” o momento imediatamente antes da colisão e “final” imediatamente após a colisão. Então para um sistema de massa total , vamos ter:
Passo 2
Substituir por valores conhecidos
Achou que tinha acabado? Não acabou não, mas não falta muito! Com a expressão encontrada no passo anterior, falta só substituir os valores! Veja:
Passo 3
(b)Conservação do momento linear para o sistema
Usamos antes a conservação do momento linear para o centro de massa do sistema de partículas, não foi? E se usássemos para o sistema todo, como ficaria? Vamos dar uma olhada nisso:
Então fica atento porque pra achar precisamos primeiro achar !
Passo 4
Decompor
Depois da colisão, o que aconteceu com a esfera ? Saca só:
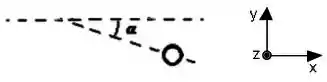
A esfera fará esse movimento, onde . Então, podemos decompor e obter:
Calma, ta acabando!! Já que conhecemos pelo enunciado, a gente termina rapidinho essa parte substituindo os números
Passo 5
Substituir por valores conhecidos
Nessa parte você se pergunta: tudo isso pra que? Vai ficar claro quando o resultado do Passo e do Passo se unirem, então dá uma olhada:
Viu só? Agora, unindo os dois resultados acima a gente consegue achar o que falta, que é . Partiu calcular então:
Passo 6
(c) Conservação da energia cinética
Seja a colisão elástica ou inelástica, vamos ter de qualquer modo a conservação do momento linear, mas nem sempre a conservação da energia cinética. Temos, no entanto, um problema ao calcular as energias cinéticas: o módulo das velocidades! O único que temos é ! O que fazer então?
Essa é a hora mágica que vamos usar pela primeira e única vez as expressões e do enunciado.Dá uma olhada nessa relação:
Pois é! Podemos derivar a posição em função do tempo para achar a velocidade das duas esferas! Então calma, que agora que identificamos isso, fica mais tranquilo. Vamos derivar então:
E então, calculamos o módulo de cada uma das velocidades:
A única velocidade na qual a gente ainda não tem o módulo é , mas não é algo que não possamos calcular, não é mesmo?
Agora que sabemos o módulo de todas as velocidades, basta substituir:
Opa, encontramos . Ou seja, a energia cinética não se conserva e a colisão então é inelástica
Resposta
a)
b)
c) Colisão Inelástica