Um toca-discos com um prato de diâmetro é posto em rotação por meio de uma correia ligada ao eixo de um motor de diâmetro . Veja a ilustração abaixo. Partindo do repouso, o prato alcança a velocidade angular final (rotações por minuto) em um intervalo de tempo Considere a correia como sendo inextensível e suponha as acelerações constantes. Resolva o problema literalmente para só no final substituir os valores numéricos.
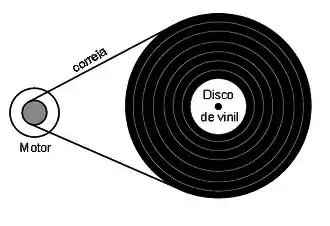
(a) Determine as acelerações angulares do motor e do prato do toca-discos.
(b) Determine quantas rotações o prato faz até atingir sua velocidade final.
(c) Determine os módulos das acelerações radial ar e tangencial at de um ponto na borda do prato após ele atingir a velocidade final.
Passo 1
(a)Obter a aceleração angular do prato
Nesse primeiro passo, basta ficar atento no enunciado pra acertar em cheio! Se o disco acelera durante saindo do repouso () para uma velocidade final , achamos a aceleração angular com a seguinte relação:
Mas calma Cowboy, não tão depressa! Se só substituir os valores vamos ter uma inconsistência dimensional. Vamos repaginar as unidades da velocidade então. Se:
Então mudando as unidades da velocidade, temos:
E a aceleração ficará:
Passo 2
Analisar o movimento da correia
Vamos começar do começo e ligar o motor que estava desligado. O que vai acontecer? Bem, se não esquecermos de ligar na tomada o motor, ele irá acelerar a correia. Então, vamos ter o seguinte esquema:
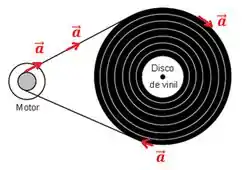
Como a correia está sendo acelerada, em todos os seus pontos a aceleração linear será igual. Aí que está o pulo do gato pra responder essa questão! Se as acelerações lineares são iguais em todos os pontos, podemos igualar as acelerações lineares para dois pontos de interesse: um em cima do disco do motor e outro em cima do disco de vinil:
Agora temos uma expressão pra aceleração angular do motor que só tem informações que conhecemos. Só substituir e ser feliz:
Passo 3
(b)Aplicar a Equação de Torricelli para movimentos circulares
Lembra das equações do movimento? Pois bem, para todos eles, incluindo a Equação de Torricelli, existe uma versão para movimentos circulares. Dá uma olhada no caso do disco de vinil:
Tá, e pra que eu quero essa fórmula? Bem, pra saber quantas voltas o disco deu até atingir a velocidade angular final a gente precisa saber quantas vezes a variação de angulação cabe em uma rotação. Assim, o número de rotações pode ser explicitado:
Opa! Agora é só substituir e partir pro abraço!
Passo 4
(c)Componentes da aceleração em movimentos circulares uniformemente variado
Cansado? Calma, está acabando, só mais essa questão! Nesse item, queremos calcular a aceleração tangencial e radial (ou centrípeta) em um movimento circular. Mas que acelerações são essas? Vamos dar uma olhada:
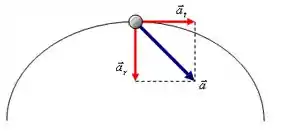
Para um ponto na borda do disco, a aceleração linear resultante vai ser a soma dessas duas componentes, certo? O módulo de cada uma das componentes vai ser:
Quando a velocidade angular final é alcançada, a correia passa a se mover em velocidade constante, beleza? Se a velocidade da correia é constante, a velocidade do ponto na borda do prato também será, e substituindo, temos:
Resposta
a)
b)
c)