P2 de Física B - FIS1026 da PUCRIO - 2018.1

Um sistema composto por uma haste delgada de massa e comprimento e um aro fino de raio desconhecido e mesma massa é livre para girar em torno do eixo . Determine, fornecendo as respostas com o número de algarismos significativos adequado:

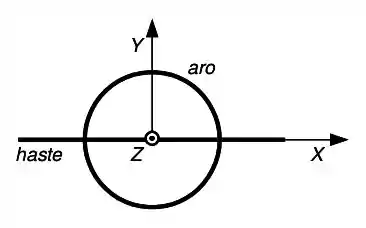
a) O valor de que faz o momento de inércia do aro ser igual ao momento de inércia da haste.

b) Determine a aceleração angular necessária para levar o sistema do repouso até que um ponto na extremidade da haste possua velocidade tangencial em

c) Suponha agora que o momento de inércia do conjunto seja e que ele gire com velocidade angular . Determine o trabalho necessário para levar o sistema ao repouso completo

d) Se o eixo de rotação for movido paralelamente até a extremidade da haste qual o novo momento de inércia do conjunto neste novo eixo?

Dados:

Considere uma partícula de massa se movendo com uma velocidade desconhecida . Essa partícula sofre uma colisão com uma segunda partícula de massa inicialmente em repouso, permanecendo ambas as massas unidas depois da colisão, com uma velocidade . Chame essa nova partícula de .

a) Calcule o valor de

b) Calcule a variação de energia cinética dessa colisão

Essa nova partícula colide com uma terceira partícula de massa inicialmente em repouso. Imediatamente após a colisão, a velocidade da partícula é .

c) Calcule os momentos lineares da partícula e da partícula , imediatamente após a colisão: e

d) Calcule as energias cinéticas do sistema composto pelas partículas e , imediatamente antes e imediatamente antes e imediatamente depois da segunda colisão: e . Essa colisão foi elástica ou inelástica?

A figura abaixo mostra o gráfico aproximado do módulo da força em função do tempo para a colisão de uma bola de massa contra uma parede. O valor do módulo da força máxima é desconhecido. A velocidade da bola imediatamente antes da colisão é , perpendicular à parede. A bola ricocheteia praticamente com o mesmo módulo da velocidade também perpendicular à parede.

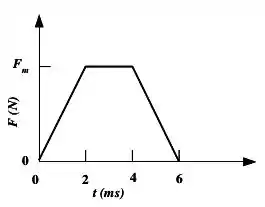
a) Calcule o impulso fornecido pela parede sobre a bola

b) Calcule o módulo da força máxima

Seja um objeto de massa colocado no topo de um plano inclinado fixo de massa , base e altura . Considere o objeto como uma massa pontual e despreze o atrito entre o objeto e o plano inclinado.

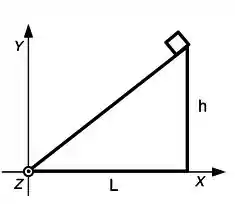
a) Determine a posição do centro de massa do conjunto (objeto + plano inclinado) na posição ao lado, antes do objeto ser solto. A posição do centro de massa do plano inclinado é dado por .

b) O objeto é largado do repouso de desce o plano inclinado. Determine a velocidade do centro de massa do conjunto imediatamente antes do objeto sair do plano inclinado.