Seja um objeto de massa colocado no topo de um plano inclinado fixo de massa , base e altura . Considere o objeto como uma massa pontual e despreze o atrito entre o objeto e o plano inclinado.
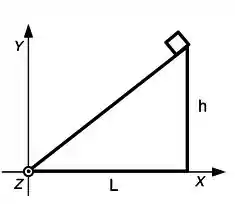
a) Determine a posição do centro de massa do conjunto (objeto + plano inclinado) na posição ao lado, antes do objeto ser solto. A posição do centro de massa do plano inclinado é dado por .
b) O objeto é largado do repouso de desce o plano inclinado. Determine a velocidade do centro de massa do conjunto imediatamente antes do objeto sair do plano inclinado.
Passo 1
a)
A posição do objeto é dada, segundo a figura, por
E a posição do centro de massa do plano inclinado é
O centro de massa do sistema então será
Passo 2
b)
Antes de sair do plano inclinado o bloco terá uma velocidade que podemos obter por conservação de energia. Inicialmente o bloco só tem energia potencial gravitacional e na base do plano o bloco tem somente energia cinética, assim
Passo 3
Calculamos o módulo da velocidade, só que precisamos do vetor velocidade. Esse vetor tem que está na mesma direção do plano inclinado.
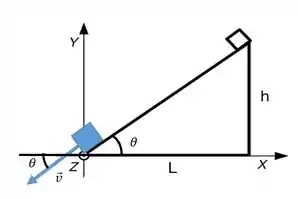
As componentes e desse vetor obedece as mesmas relações métricas que o triângulo retângulo do plano inclinado
A hipotenusa desse plano inclinado é
Assim
Finalmente a velocidade do objeto será
Passo 4
Como o plano está parado, a sua velocidade será zero
Assim a velocidade do centro de massa do sistema será
Resposta
a)
b)