Um sistema composto por uma haste delgada de massa e comprimento e um aro fino de raio desconhecido e mesma massa é livre para girar em torno do eixo . Determine, fornecendo as respostas com o número de algarismos significativos adequado:
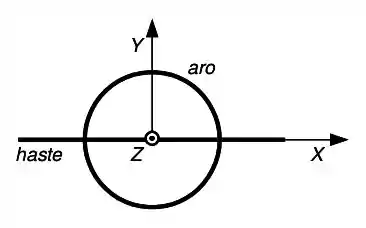
a) O valor de que faz o momento de inércia do aro ser igual ao momento de inércia da haste.
b) Determine a aceleração angular necessária para levar o sistema do repouso até que um ponto na extremidade da haste possua velocidade tangencial em
c) Suponha agora que o momento de inércia do conjunto seja e que ele gire com velocidade angular . Determine o trabalho necessário para levar o sistema ao repouso completo
d) Se o eixo de rotação for movido paralelamente até a extremidade da haste qual o novo momento de inércia do conjunto neste novo eixo?
Dados:
Passo 1
a)
O momento de inércia do aro é dado por
E o momento de inércia da haste é dada por
Onde a massa da haste é igual a massa do aro, como disse o enunciado.
Queremos que os dois momentos sejam iguais
Passo 2
b)
Um ponto da extremidade da haste executa um movimento circular de raio . Podemos relacionar o raio desse movimento circular com a velocidade angular e a velocidade linear por
A frequência inicial então será
Passo 3
A função horária da velocidade angular é dada por
Como queremos para
Passo 4
c)
A energia cinética de um sistema rotacionando é dada por
A frequência angular se relaciona com a frequência por
Assim
O enunciado deu em mas precisamos dela em . Pra isso
Inicialmente essa energia cinética é dada por
Já quando o conjunto está em repouso a sua energia é nula
Pelo teorema trabalho energia cinética
Passo 5
d)
O conjunto todo tem massa . O momento de inércia no novo eixo é dado pelo teorema dos eixos paralelos onde deslocamos uma distância
Resposta
a)
b)
c)
d)