A figura abaixo mostra o gráfico aproximado do módulo da força em função do tempo para a colisão de uma bola de massa contra uma parede. O valor do módulo da força máxima é desconhecido. A velocidade da bola imediatamente antes da colisão é , perpendicular à parede. A bola ricocheteia praticamente com o mesmo módulo da velocidade também perpendicular à parede.
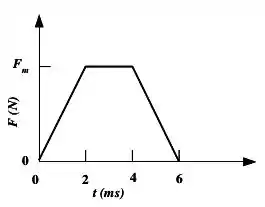
a) Calcule o impulso fornecido pela parede sobre a bola
b) Calcule o módulo da força máxima
Passo 1
a)
O enunciado diz que o módulo da velocidade da bola após a colisão é igual ao módulo da velocidade antes da colisão, ou seja
Para calcular o impulso, basta lembrar que a relação entre impulso e variação de momento linear por
Passo 2
b)
O impulso é dado por
Como temos um gráfico de por , o módulo do impulso será a área do nosso gráfico. Podemos dividir essa figura em dois triângulos e um retângulo
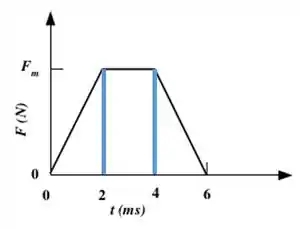
A área total será
Como já vimos que
Resposta
a)
b)