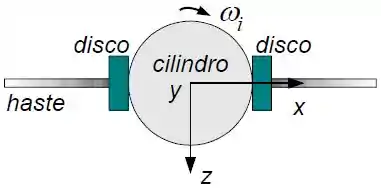
Considere um sistema composto por um cilindro de massa e raio , uma haste de massa e comprimento e dois discos de massa . Os discos estão encostados no cilindro, presos por um freio, como ilustra a figura. Um torque externo coloca o sistema em rotação em torno do eixo-y no sentido horário sendo desligado quando a velocidade angular é alcançada. Neste instante o freio que prende os discos é retirado e os discos deslizam pela haste até as suas extremidades.
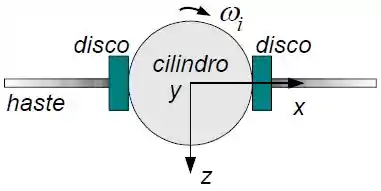
a) Encontre a nova velocidade angular do sistema quando os discos chegarem nas extremidades da haste. Considere os discos como massas pontuais.
Dados: sendo:
;
;
;
;
Passo 1
Basicamente o encunciado diz que esse sistema está girando com uma velocidade quando a trava dos discos é retirada e eles escorregam até a extremidade da barra.
Mas repara que não houve nenhum torque externo sobre o sistema. Assim, o Momento Angular se conserva:
Como o momento de inércia muda conforme os discos escorregam para a extremidade, a velocidade angular também vai mudar.
Então, a questão basicamente é encontrar os momentos de inércia inicial e final e aplicar na conservação do Momento Angular.
Passo 2
O momento de inércia inicial será:
Como os dois discos estão a uma mesma distância do eixo de rotação, eles têm o mesmo momento de inércia.
No formulário temos o momento de inércia para cada um desses caras. Mas precisamos saber com relação a qual eixo de rotação essas fórmulas se referem.
Para o cilindro a fórmula se refere a um eixo assim:
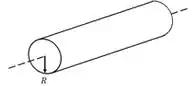
Então ok, podemos usar!
Para a haste, a fórmula se refere a um eixo assim:
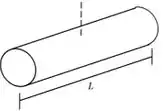
Então ok, também podemos usar!
Já para o disco, a fórmula se refere a um eixo passando pelo seu centro:
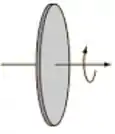
Não é o que acontece, então a fórmula não se aplica ao caso.
Os dois discos no sistema estão como partículas afastadas de uma distância do eixo de rotação, então o momento de inpercia será:
Somando tudo, temos:
Passo 3
Já na nova configuração, temos que o momento de inércia será:
Onde e são os mesmos, porém o é o momento de inércia dos discos na extremidade da haste.
A distância da extremidade da haste ao eixo de rotação é igual a metade do comprimento da haste, ou seja, .
Calculando :
Passo 4
Agora, só falta substituir na conservação de momento angular:
Cortando o termo dos dois lados, achamos que: