O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.
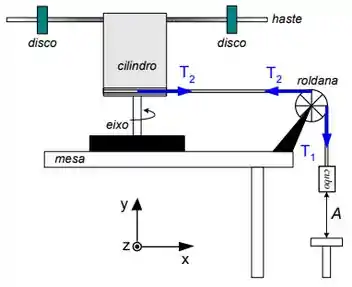
(d) Determine a energia cinética adquirida pelo sistema desde até quando o cubo está prestes a encostar no suporte. Despreze atritos.
Passo 1
Quando o freio é retirado, o bloquinho começa a descer devido à ação da gravidade.
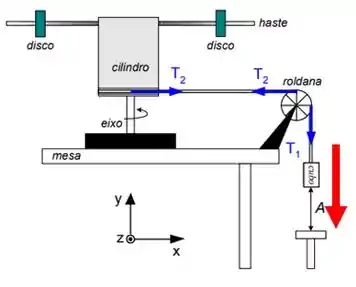
E consequentemente, ele puxa a corda que faz a roldana e aquele objeto estranho entrarem em rotação.
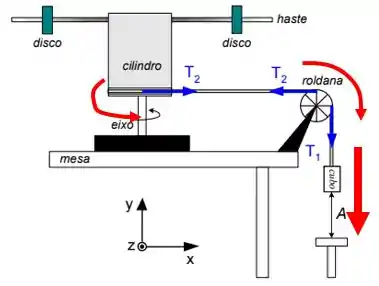
Queremos saber a energia cinética do sistema após o bloco descer uma altura .
Como não há atrito, a energia mecânica do sistema se conserva:
Então, a energia potencial do boquinho vai se transformar em energia cinética.
Essa energia cinética estará na forma de cinética de rotação da roldana e do objeto, mas também de cinética de translação do próprio bloquinho.
Mas não precisamos diferenciar cada energia cinética nessa questão, queremos apenas a total.
Passo 2
Então, a conservação de energia fica:
É só isso mesmo:
Ou seja, toda a energia potencial do bloquinho se transformou em energia cinética quando ele desceu uma altura até o suporte.
Resposta
(d)