Considere um carretel de raio externo , massa e momento de inércia em relação ao centro de massa . Ele está em repouso quando uma corda enrolada no cilindro interno de raio é puxada com uma força de tração horizontal constante . O carretel passa a rolar sem deslizar no sentido horário (para a direita) em um plano horizontal com coeficiente de atrito estático . As forças na direção horizontal, atrito e tração, agindo no carretel estão ilustradas na figura.
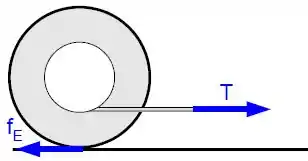
a) Escreva as equações de movimento que descrevem a dinâmica do carretel como translação do centro de massa e rotação em torno do centro de massa.
b) Use as equações do item anterior para obter o modulo da aceleração angular α em relação ao centro de massa do carretel.
c) Qual é o valor máximo da tração para o rolamento sem deslizamento.
Passo 1
Vamos começar com as equações de movimento.
Esse carretel terá tanto um movimento de translação quanto um movimento de rotação.
Começando com a Segunda Lei de Newton para translação:
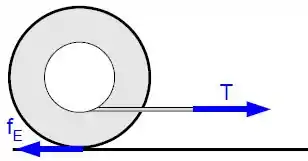
Passo 2
A Segunda Lei de Newton para rotação fica:
O vetor posição é perpendicular ao vetor força nos dois casos:
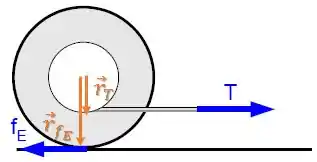
Então, o módulo dos torques serão o raio vezes a força.
Para a força , o raio do cilindro interno é e para a força de atrito , o raio do cilindro externo é :
Como o cilindro gira no sentido horário, a aceleração angular está nesse sentido. Vamos considerar esse sentido como positivo.
O torque da força de tração tenta girar no sentido anti-horário (negativo) enquanto o torque da força de atrito tenta girar no sentido horário (positivo):
Sabemos também o momento de inércia , dado no enunciado:
Pronto, temos a nossa segunda equação de movimento.
Passo 3
Na letra (b), queremos a aceleração angular .
Para isso vamos usar aquelas duas equações que achamos:
Mas existe mais uma relação que podemos utilizar.
Como não há deslizamento entre o carretel e o chão, necessariamente a aceleração do centro de massa se relaciona com a aceleração angular a partir de:
Vamos substituir isso na primeira equação:
Além disso, vamos simplificar a segunda equação cortando o dos dois lados:
Passo 4
Agora nosso sistema ficou:
Como não é um valor conhecido, vamos eliminá-lo da resposta.
Podemos simplesmente somar as duas equações:
Passo 5
Na letra (c), queremos o valor máximo de tração sem que haja deslizamento.
Qual é a situação limite sem que haja deslizamento?
É quando a força de atrito estático atinge seu valor máximo:
Passo 6
Usando a Segunda Lei de Newton para translação, temos:
Então, quando a força de atrito estiver em seu valor máximo, teremos :
Agora, vamos deixar essa expressão apenas em função de parâmetros conhecidos.
Passo 7
Como o carretel está em equilíbrio na vertical, temos que a força normal é igual à força peso:
Substituindo na nossa equação:
Passo 8
Além disso, sabemos que a aceleração é igual a:
Substituindo isso na expressão:
Isolando o :
Resposta
(a)
(b)
(c)