O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.
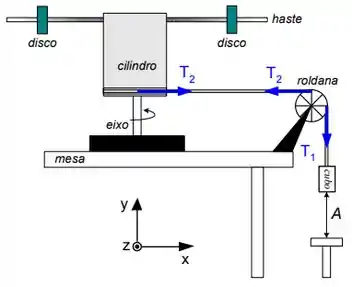
a) Em função das forças indicadas na ilustração, escreva os torques que agem na roldana e no objeto no instante .
Passo 1
Num primeiro momento, essa figura pode parecer meio complicada. Mas fica tranquilo que não é nada demais.
Quando o freio é retirado, o bloquinho começa a descer devido à ação da gravidade.
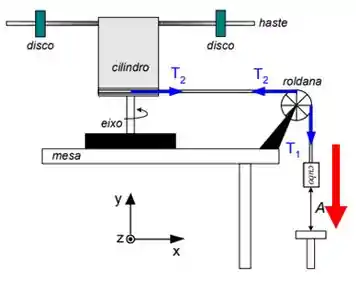
E consequentemente, ele puxa a corda que faz a roldana e aquele objeto estranho entrarem em rotação.
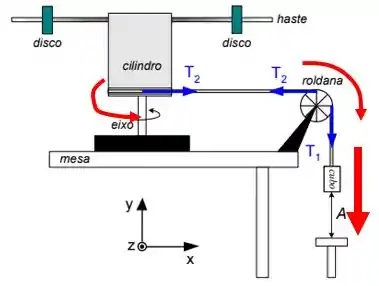
Sacou o que tá “rolando”?
Hahahh, okay, parei.
Passo 2
Na letra (a), queremos os vetores do torque sobre a roldana e sobre o objeto .
Queremos os VETORES torque...
Ou seja, além do módulo também precisamos escrever a direção e sentido a partir do sistema de referências da questão.
O vetor torque é dado pelo produto vetorial entre o vetor posição (centro de rotação até ponto de aplicação da força) e o vetor força :
Lembrando também que podemos calcular o módulo desse produto vetorial com:
Onde é o ângulo entre eles.
E se os vetores fizerem entre si temos:
Passo 3
Vamos começar com a roldana.
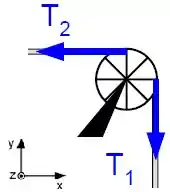
Os vetores está na direção negativa do eixo enquanto o está na direção positiva do eixo :
Já os vetores posição são:

Os módulos dos vetores (tamanho) serão seu raio :
Passo 4
Agora, vamos calcular o torque na roldana.
OBS: Produto vetorial resulta num vetor () perpendicular aos dois vetores () e (), no caso da roldana, estará na direção do eixo .
Começando com o torque da primeira força:
Pela regra da mão direita, temos:
Já o torque da segunda força é:
Pela regra da mão direita, temos:
Beleza, então o torque resultante na roldana será:
Pronto, já achamos nossa resposta.
Mas só para melhorar um pouquinho mais... como a roldana gira no sentido horário, a força é maior que a força . Ou seja, aquele termo resulta num valor negativo.
Ou seja, o torque resultante está na direção .
Então, vamos reescrevê-lo de outra forma. Vai dar no mesmo, porém, agora passa uma ideia mais clara do sentido:
Passo 5
Agora vamos fazer o mesmo procedimento para achar o torque no objeto .
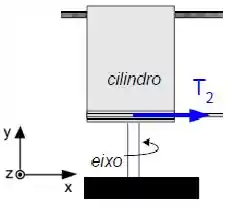
O vetor da força de tração está na direção do eixo :
Repara que o vetor posição está na direção do eixo , pois parte do centro do cilndro até o ponto de aplicação de .
Dá uma olhada no objeto por cima (vista superior), vemos isso aqui:
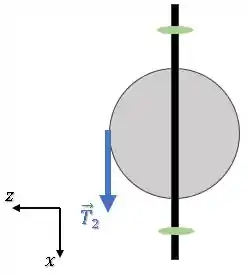
O vetor posição é esse aqui:
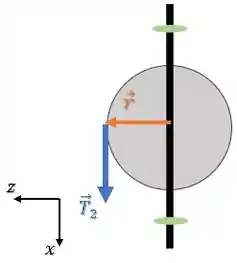
Lembrando que o raio do cilindro é (diferente da roldana).
Passo 6
O torque no objeto será:
Pela regra da mão direita, esse produto vetorial resulta na direção positiva do eixo :
Resposta
(a)