Um objeto de massa desliza na direção do eixo-x positivo em uma superfície com coeficiente de atrito cinético . O objeto tem uma velocidade quando colide de forma perfeitamente inelástica com uma mola quando ela está no seu ponto de equilíbrio (relaxada). A mola tem uma constante elástica . Durante a compressão da mola o atrito é desprezível. O objeto para momentaneamente, depois de comprimir a mola uma distância . O objeto é então forçado pela mola a se mover na direção do eixo-x negativo junto com a mola passando de novo pelo ponto de equilíbrio até parar momentaneamente a uma distância deste ponto. Considere o objeto como uma massa pontual. Utilize conservação de energia nas respostas abaixo. Justifique seus cálculos.
Dados:
a) Calcule o trabalho sobre o objeto desde o momento em que ele encosta na mola até parar momentaneamente.
b) Determine a distância d que a mola foi comprimida até parar momentaneamente.
c) Determine a velocidade quando o objeto passa pela posição de equilíbrio na volta, isto é se movendo na direção do eixo-x negativo.
d) Lembre que na volta a mola fica presa no objeto. Determine a distância D que a mola foi distendida até parar momentaneamente.
Passo 1
O enunciado diz que existe atrito, porém ele é desprezível no trecho de compressão da mola.
Na letra (a), queremos o trabalho sobre o objeto desde quando ele enconsta na mola até parar.
Podemos utilizar o Teorema Trabalho-Energia Cinética:
A energia cinética final é nula, pois o bloco está parado:
Então, basta substituirmos os valores, para encontrar o trabalho realizado sobre o bloco:
Passo 2
Agora na letra (b), queremos a distância até o bloco parar.
Vamos usar o mesmo teorema que usamos no item anterior:
Quais são as forças atuando sobre o bloco?
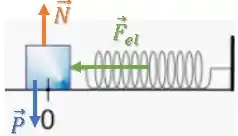
Então, o trabalho resultante será a soma do trabalho de cada uma dessas forças:
O bloco se desloca na horizontal. Como e são perpendiculares ao deslocamento, elas não geram trabalho:
Enquanto isso, a força elástica (para esquerda) está contrária ao deslocamento do bloco (para direita), então seu trabalho será negativo.
O trabalho da força elástica é dado pela expressão:
Se o deslocamento até o bloco parar foi igual a , temos:
Passo 3
Na letra (c), queremos o vetor velocidade quando o bloco volta à posição de equilíbrio.
Pensa comigo...
Não há atrito nesse trecho de ida e volta da mola até o ponto de equilíbrio, certo?
Então nenhuma energia foi dissipada.
O que aconteceu foi que a energia cinética inicial foi convertida em energia potencial elástica até que o bloco chegou na compressão máxima da mola e parou.
Depois disso, a energia potencial elástica foi convertida novamente em energia cinética do bloco conforme a mola foi sendo distendida.
Então o bloco voltou a ter a mesma energia cinética e portanto o mesmo módulo da velocidade inicial , com a única diferença no sentido do vetor.
Agora o bloco está voltando no sentido negativo do eixo-x, então a sua velocidade é:
Passo 4
Na letra (d), queremos a distância D que a mola foi distendida até que o bloco pare momentaneamente.
Agora, muito cuidado!
Estamos na região onde o atrito deve ser considerado.
Felizmente, podemos usar o mesmo teorema que usamos antes, com a única diferença que agora existe um trabalho da também.
Dá uma olhada nas forças atuando sobre o bloco agora.
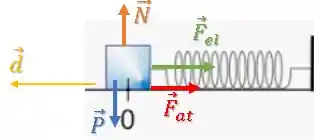
O deslocamento do bloco é para a direita ().
A mola está sendo esticada então a força elástica está puxando o bloco.
A força de atrito está contra o delizamento, então também está para a direita.
Passo 5
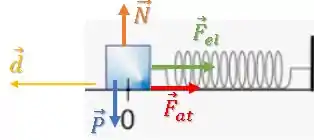
As forças peso e normal são perpendiculares ao deslocamento e por isso não geram trabalho:
O trabalho da força elástica será negativo, pois essa força está contrária ao deslocamento. Além disso, a deformação da mola será a distância :
O trabalho da força de atrito também será negativo, pois essa força está contrária ao deslocamento. E será dada por:
Passo 6
Como há um equilíbrio na vertical, a força normal é igual ao peso:
Então:
Passo 7
Agora, vamos às energias cinéticas.
A energia cinética final será nula pois é o momento em que o bloco para.
E a energia cinética inicial será aquela quando o bloco tem velocidade que calculamos no item (c):
Mãos à obra! Vamos substituir os valores.
Multiplicando tudo por :
Isso mesmo, vamos ter que usar aquele famoso Bháskara para resolver essa equação de segundo grau.
Passo 8
Vamos achar as raízes.
Calculando o :
Então, temos:
Como estamos procurando um número positivo, temos:
Resposta
(a)
(b)
(c)
(d)