Com , determine a impedância de entrada do circuito abaixo:
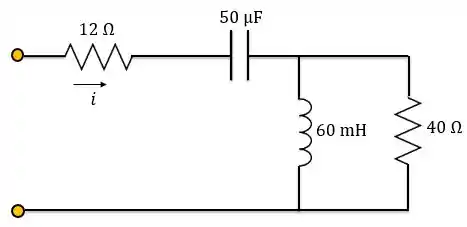
Passo 1
A impedância de entrada do circuito será:
Onde é a impedância equivalente entre o paralelo da reatância indutiva com resistência de .
Vamos primeiro calcular as reatâncias do circuito.
Passo 2
Agora precisaremos calcular o paralelo entre a reatância indutiva e a resistência:
Passando a reatância para a forma polar, teremos que:
Então:
Passando o denominador para a forma polar:
Logo:
Passo 3
Passando a impedância equivalente 1 para a forma retangular:
Passo 4
Já temos todos os dados para calcular a impedância de entrada:
Resposta
Exercícios de Livros Relacionados
Obtenha a impedância equivalente para o circuito da Figura 9.78.
a Calcule o deslocamento de fase do circuito da Figura 9.82. b Informe se o deslocamento de fase está avançado ou atrasado (saída em relação à entrada). c Determine a magnitude da saída quando a entra
Uma ponte de capacitância está equilibrada quando R 1 = 1 00Ω ,R 2 = 2 k ΩeC s = 40μ F . Qual o valor de C x , a capacitância do capacitor em teste?
55- Determine Z no circuito da Figura 9.62 dado que V_o = 4 /_ 0 ° V
O circuito da Figura 9.87 faz parte do esquema que descreve um sensor eletrônico industrial. Qual é a impedância total do circuito em 2k H z ?