Determine no circuito abaixo. Considere .
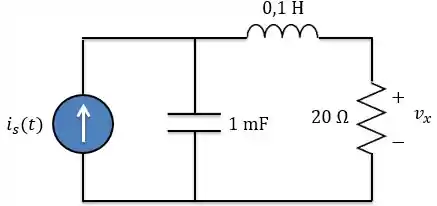
Passo 1
Nosso primeiro passo é passar o circuito para o domínio da frequência para podermos trabalhar com fasores.
Primeiro a corrente. Como ela já está na forma de cosseno, a transformação é direta:
Calculando as reatâncias do circuito.
Passo 2
Logo, podemos estudar o circuito da seguinte forma:
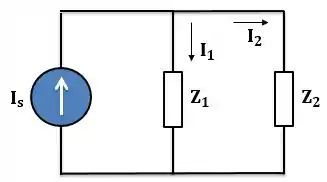
Passo 3
Lembrando que tudo o que vimos para resistores é válido para impedâncias, já que também é válida as leis de Kirchhoff quando utilizamos fasores. Aplicando divisor de corrente, temos:
Passo 4
Como passa pelo resistor de , aplicando a lei de Ohm, temos:
Agora é só voltar para o domínio do tempo:
Resposta
Exercícios de Livros Relacionados
Obtenha a impedância equivalente para o circuito da Figura 9.78.
a Calcule o deslocamento de fase do circuito da Figura 9.82. b Informe se o deslocamento de fase está avançado ou atrasado (saída em relação à entrada). c Determine a magnitude da saída quando a entra
Uma ponte de capacitância está equilibrada quando R 1 = 1 00Ω ,R 2 = 2 k ΩeC s = 40μ F . Qual o valor de C x , a capacitância do capacitor em teste?
55- Determine Z no circuito da Figura 9.62 dado que V_o = 4 /_ 0 ° V
O circuito da Figura 9.87 faz parte do esquema que descreve um sensor eletrônico industrial. Qual é a impedância total do circuito em 2k H z ?