Determine a admitância para o circuito abaixo:
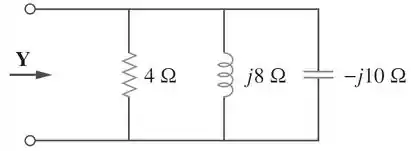
Passo 1
A admitância do circuito será dada por:
Temos três impedâncias no circuito acima:
Passo 2
Como as impedâncias estão em paralelo, a impedância equivalente será dada por:
Passo 3
Como será necessário fazer divisão, vamos passar as impedâncias para a forma polar:
Passo 4
Calculando a impedância equivalente:
Passo 5
Agora, como vamos ter que somar, teremos que passar cada parcela da impedância equivalente para a forma retangular. Lembrando que:
Logo:
Passo 6
A admitância é, então:
Resposta
Exercícios de Livros Relacionados
Obtenha a impedância equivalente para o circuito da Figura 9.78.
a Calcule o deslocamento de fase do circuito da Figura 9.82. b Informe se o deslocamento de fase está avançado ou atrasado (saída em relação à entrada). c Determine a magnitude da saída quando a entra
Uma ponte de capacitância está equilibrada quando R 1 = 1 00Ω ,R 2 = 2 k ΩeC s = 40μ F . Qual o valor de C x , a capacitância do capacitor em teste?
55- Determine Z no circuito da Figura 9.62 dado que V_o = 4 /_ 0 ° V
O circuito da Figura 9.87 faz parte do esquema que descreve um sensor eletrônico industrial. Qual é a impedância total do circuito em 2k H z ?