Determine no circuito RLC da figura
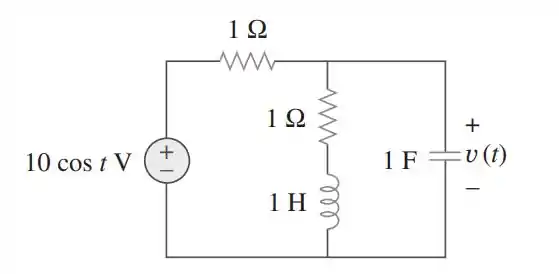
Passo 1
Vamos passar logo a nossa fonte para a forma fasorial polar
Agora vamos achar as reatâncias dos elementos passivos para
Passo 2
Agora vamos redesenhar o circuito mostrando as impedâncias no domínio complexo::
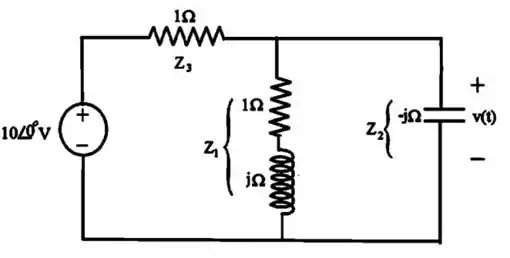
Passo 3
A partir dessa figura, vemos que temos 3 impedâncias,
Para achar , vamos somar:
E, em seguida, vamos fazer o paralelo de com :
Passo 4
Agora, observe que a tensão que passa pelas impedâncias em paralelo é a mesma que passa pelo capacitor, porque eles estão em paralelo. Então, podemos utilizar divisor de tensão para achar
(aqui, note que usamos o valor da impedância na forma polar)
(passando para a forma polar…)
Passando para o domínio do tempo, teremos:
Resposta
Exercícios de Livros Relacionados
Obtenha a impedância equivalente para o circuito da Figura 9.78.
a Calcule o deslocamento de fase do circuito da Figura 9.82. b Informe se o deslocamento de fase está avançado ou atrasado (saída em relação à entrada). c Determine a magnitude da saída quando a entra
Uma ponte de capacitância está equilibrada quando R 1 = 1 00Ω ,R 2 = 2 k ΩeC s = 40μ F . Qual o valor de C x , a capacitância do capacitor em teste?
55- Determine Z no circuito da Figura 9.62 dado que V_o = 4 /_ 0 ° V
O circuito da Figura 9.87 faz parte do esquema que descreve um sensor eletrônico industrial. Qual é a impedância total do circuito em 2k H z ?