Determine a corrente no circuito abaixo quando .
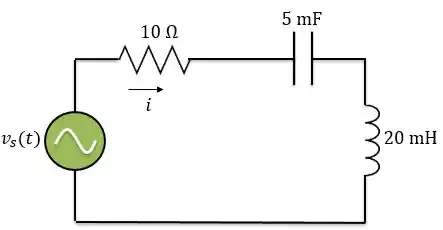
Passo 1
Para determinar a corrente nesse exercício, vamos trabalhar com fasores e teremos que encontrar a impedância do circuito, porque a corrente será:
Como temos um capacitor e um indutor, calcularemos a reatância capacitiva e reatância indutiva, já que como esses elementos estão em série a impedância será:
Passo 2
Lembrando que através da equação fornecida da tensão, podemos encontrar a frequência angular :
Logo, .
Calculando a reatância capacitiva, fazemos:
Calculando a reatância indutiva, fazemos:
Passo 3
Agora já podemos calcular a impedância:
Passo 4
Como vamos precisar dividir a tensão pela impedância para calcular a corrente, temos que passar ambas as grandezas para a forma polar.
Primeiro a tensão. Como ela já está na forma de cosseno, a transformação é direta:
Agora a impedância. Você lembra como fazemos para passar para a forma polar? Primeiro a gente tem que achar o módulo:
O ângulo será:
Portanto, a impedância na forma polar é:
Passo 5
Finalmente podemos calcular a corrente:
Agora é só voltar para o domínio do tempo: