No circuito da figura, determine o valor de .
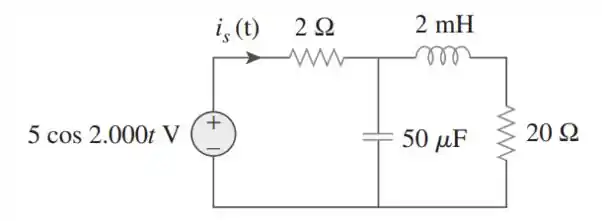
Passo 1
Vamos calcular nossas impedâncias sabendo que (basta olhar para a tensão)
Passo 2
Agora, vamos calcular a impedância equivalente do circuito para poder calcular a corrente.
Então, a corrente será:
Então, no domínio do tempo teremos: