Para o carregamento mostrado, determinar: (a) a equação da curva elástica para a viga ; (b) a deflexão da extremidade livre; (c) a declividade da extremidade livre. Assuma constante.
Passo 1
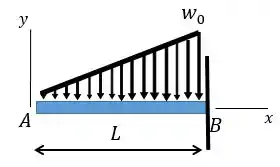
Fala, galerinha!!! Aqui o problema nos fornece uma viga engastada em e livre em e submetida a um carregamento triangular conforme mostrado. Como existe um carregamento distribuído a gente pode utilizar direto a equação que relaciona carregamento com deflexão:
Dessa forma o mais importante para a gente agora é encontrar a função que define o carregamento e definir o sentido do eixo .
Passo 2
Primeiro vamos definir o sentido do eixo , essa parte é muito importante ok? A nossa questão até já deixou meio indicado mas vou mostrar para vocês qual foi adotado:
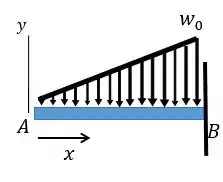
Ou seja, vamos varrer nossa viga da esquerda para a direita.
Para definir a função do carregamento a gente só precisa lembrar que essa é uma função linear que se inicia no ponto e termina em , com isso vamos obter:
Perceba que o valor de é, por exemplo:
Faz sentido né?
Passo 3
Agora vamos resolver a integral:
Substituindo
Integrando a primeira vez:
Se escrevermos da seguinte forma vamos ter o valor da força cortante:
Com isso podemos achar o valor da constante pois a força cortante no ponto é zero. Logo,
Passo 4
Continuando a resolução da equação e fazendo a segunda integral:
E vamos obter:
Novamente vamos poder escrever como algo que conhecemos que é o momento fletor:
E novamente o momento fletor em é igual a zero, logo:
Passo 5
Agora vamos integrar pela terceira vez:
Agora a gente tem que lembrar que o termo é igual à angulação . Assim, podemos escrever:
Não sabemos qual a angulação da extremidade livre, mas sabemos qual é a angulação da extremidade engastada (que é zero). Logo podemos substituir e :
Como o problema também pede a inclinação na extremidade livre podemos fazer e obter:
Passo 6
Agora vamos para a nossa quarta e última integral:
E finalmente achamos a equação da linha elástica:
Mas ainda falta achar o valor de e para isso utilizamos o valor da deflexão no engaste, que é zero. Logo:
E finalmente obtemos a equação da linha elástica:
Para achar a deflexão na extremidade livre é só substituir
Pronto! Problema resolvido =D
Resposta
a)
b)
c)