Determine a linha elástica para a viga simplesmente apoiada utilizando a coordenada onde . Determine também a inclinação em e a deflexão máxima da viga. é constante.
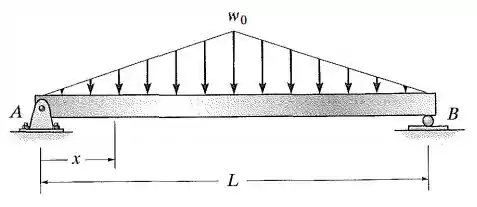
Passo 1
Nesta questão a gente tem que achar a linha elástica, a forma mais fácil para esse tipo de problema, que nos fornece o carregamento é realizar como:
Passo 2
Então o primeiro problema que encontramos é definir o carregamento como uma função em . Esse carregamento é triangular e, portanto, aumenta linearmente. Logo, pode ser descrito como:
Como o valor inicial do carregamento é igual a zero, então o termo .
Agora se aplicarmos essa função no ponto vamos obter o valor de , assim:
Sendo assim,
E o nosso carregamento pode ser dado por:
Passo 3
Agora vamos aplicar a equação da linha elástica:
Podemos reorganizar da forma:
Aí é só ir derivando rs. A primeira derivada temos:
Derivando novamente:
Derivando pela terceira vez:
Derivando pela quarta e última vez:
Agora é só achar as quatro constantes!
Passo 4
Pessoal, para achar essas constantes a gente tem que reparar que cada uma delas, por estar associada a cada etapa de integração, vai estar associada aos termos da força cortante, momento fletor, inclinação e deflexão.
Vamos um pouco mais devagar. Lá na primeira integral a gente tinha:
O termo da esquerda é a primeira integral de logo é igual à força cortante e podemos escrever:
Logo se a gente conseguir achar a força cortante em algum ponto da nossa viga vamos poder achar !
A cortante num ponto bem próximo de vai ser igual à própria reação em . Podemos calcular a reação em como sendo metade da força aplicada sobre a viga.
Como essa força é dada pela carga distribuída, vamos ter:
Pessoal, reparem que eu peguei só a força do triângulo da esquerda (carga vezes distância). Por que eu fiz isso? Porque queria metade da força uai!
Então para vamos ter:
Logo,
Passo 5
Agora vamos para a segunda integral, já considerando o valor de :
Essa integral se refere ao momento fletor e pode ser escrita como:
O momento fletor num ponto bem próximo do apoio será igual a zero, portanto:
Passo 6
Agora vamos para a terceira integral, já considerando os valores de e :
Essa integral se refere à inclinação e pode ser escrita como:
Agora temos de utilizar aquela propriedade de que o ângulo no ponto médio de uma viga com carregamento simétrico é nulo! Portanto em vamos ter . Assim,
Passo 7
Agora vamos para a quarta integral, já considerando os valores de , e :
Essa integral se refere à linha elástica!!
Vamos aplicar a condição de contorno onde a deflexão no apoio é nula, logo em temos que . Portanto,
Desta forma vamos ter que a linha elástica é dada por:
Que pode ser escrito como: