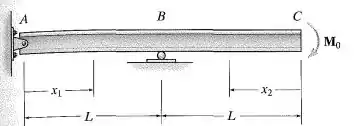
Determine a equação da linha elástica para a viga utilizando as coordenadas e e especifique a inclinação em . é constante.
Passo 1
Pessoal, nada de novo no horizonte. O problema pede a equação da linha elástica e a inclinação em , . Para tal a gente vai precisar da nossa equaçãozinha:
E como na maior parte das vezes vamos calcular o momento fletor na viga =D
Passo 2
Para achar o momento fletor primeiro precisamos achar as forças nos apoios, para isso vamos desenhar um esquema de forças.
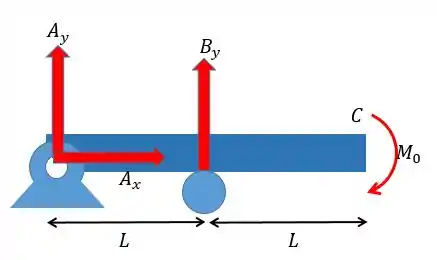
Pelas equações da estática vamos ter:
Como só temos uma força em vamos ter:
Para as forças em :
Para o momento sendo aplicado em e considerando positivo o sentido horário vamos ter:
Da equação em a gente pode achar que:
Passo 3
Com as forças vamos poder achar o momento fletor. Desenhando o corte da primeira seção vamos ter:
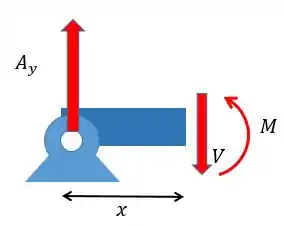
Fazendo o somatório das forças em de modo a achar a força cortante:
Agora podemos achar o momento fletor, fazendo o somatório dos momentos em torno do ponto e considerando o sentido horário positivo:
Uhulll achamos o momento!! Agora vamos achar a linha elástica!!
Passo 4
Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:
Substituindo :
Agora vamos integrar em :
Integrando novamente vamos ter:
Agora temos de utilizar as condições de contorno para obter e .
Passo 5
Lembrando que as condições são as seguintes:
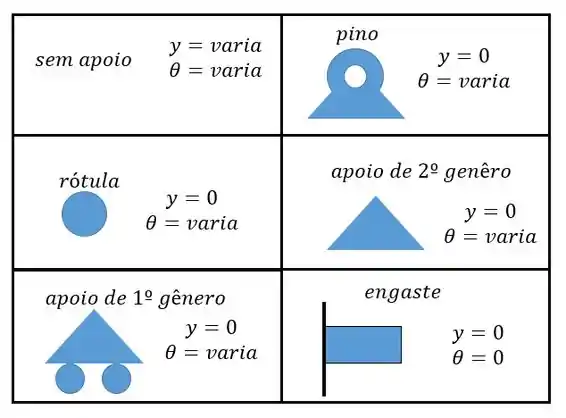
Ao aplicar essas condições no pino () vamos ter um :
Logo,
Portanto a equação fica da forma:
Agora vamos aplicar na rótula em onde , nesse ponto a deflexão também é zero, logo:
Então a equação da linha elástica é igual a:
Que pode ser escrita como:
Passo 6
Para achar a inclinação em basta utilizar a equação da inclinação lembrando que :
Em então vamos ter:
Passo 7
O problema também pediu para acharmos a equação da linha elástica ao lado direito da rótula. Isso faz sentido porque a equação que achamos é válida apenas para o trecho entre o pino e a rótula.
Para fazer isso vamos desenhar um corte dessa seção:
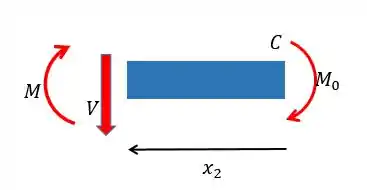
Olhando esse desenho prodemos perceber que existe apenas uma força, logo ela é nula. Assim
Com relação aos momentos, para que o corpo permaneça em equilíbrio ele deve ter os momentos iguais em módulo mas sentido opostos:
Tranquilo né? O momento fletor desse trecho é igual ao próprio momento puro aplicado só que no sentido oposto.
Passo 8
Agora é só utilizar a equação da linha elástica:
Derivando uma vez vamos ter:
Derivando novamente:
Agora só precisamos achar as contantes.
Passo 9
Deste lado da viga temos apenas uma condição de contorno. A condição de que não há deflexão no ponto onde sendo assim:
Mas ainda temos duas incógnitas e uma equação, então como vamos proceder?
Na verdade temos mais uma condição de contorno sim, só que está implícita num princípio da continuidade.
Ou seja, se calcularmos a inclinação em por meio da seção esquerda da viga, essa inclinação deve ser igual à calculada pelo lado direito!!
Sendo assim vamos ter, do lado esquerdo:
Lembrando que e substituindo os valores de vamos obter:
Agora se fizermos para a seção do lado direito:
Substituindo
Como os dois valores de são iguais:
Agora podemos substituir lá na equação:
Finalmente podemos substituir na equação da linha elástica:
É possível até verificar substituindo e verificando que =D