Uma viga engastada está sujeita a uma carga conforme o desenho abaixo. Considerando constante encontre a equação da linha elástica.
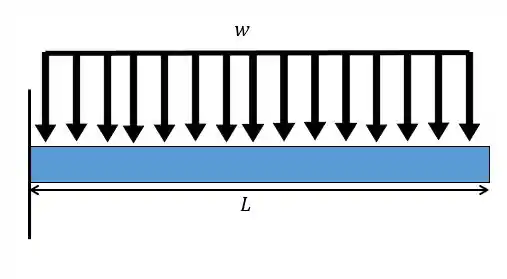
Passo 1
Pessoal esse problema é muito parecido com o anteior e a gente tem que achar a linha elástica também. Para isso, como sabemos, precisamos achar primeiro o momento fletor antes e aplicar na equação da linha elástica:
O que vai mudar aqui vai ser a forma de calcular o momento fletor, vamos fazer isso por meio de integral!
Lembrando que temos de utilizar as condições de contorno dadas por aquela nossa tabelinha:
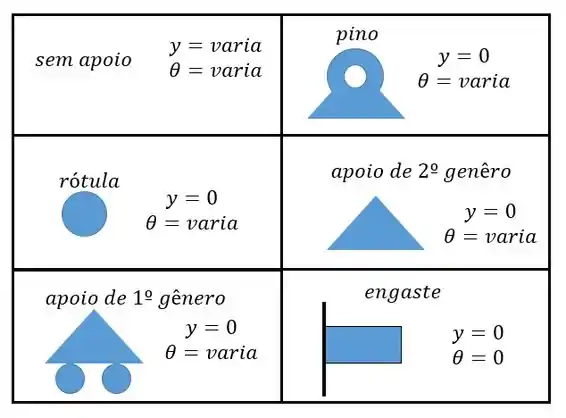
Passo 2
Galera, vocês devem lembrar que a força cortante é a derivada do momento fletor. Se não lembravam agora vocês sabem =P
Além disso, a carga distribuída é a derivada da força cortante. Então a gente tem o seguinte olha só:
Esse sinal de menos é muito importante ok? Não podemos esquecer! Ele aparece porque a cortante tem o sentido oposto do carregamento.
Então, a gente pode falar que:
Né? É só derivar o momento fletor duas vezes que vamos ter a carga.
Mas pessoal a equação da linha elástica não é dada por:
Então a gente pode derivar duas vezes e vamos ter:
Agora podemos substituir o termod a direita pelo carregamento e obter:
Desta forma podemos achar a linha elástica diretamente do carregamento
Passo 3
Aplicando esse conceito ao problema vamos ter:
Podemos reorganizar da forma:
Aí é só ir derivando rs. A primeira derivada temos:
Derivando novamente:
Derivando pela terceira vez:
Derivando pela quarta e última vez:
Agora é “só” achar as quatro constantes rs

Passo 4
Pessoal, para achar essas constantes a gente tem que reparar que cada uma delas, por estar associada a cada etapa de integração, vai estar associada aos termos da força cortante, momento fletor, inclinação e deflexão.
Vamos um pouco mais devagar. Lá na primeira integral a gente tinha:
O termo da esquerda é a primeira integral de logo é igual à força cortante e podemos escrever:
Logo se a gente conseguir achar a força cortante em algum ponto da nossa viga vamos poder achar !
Na extremidade livre não temos força cortante, portanto:
Tranquilo né?
Passo 5
Agora vamos para a segunda integral, já considerando o valor de :
Essa integral se refere ao momento fletor e pode ser escrita como:
Vamos aplicar o mesmo conceito e, ao perceber que também não existe momento fletor na extremidade livre, vamos obter:
Passo 6
Agora vamos para a terceira integral, já considerando os valores de e :
Essa integral se refere à inclinação e pode ser escrita como:
Vamos aplicar o mesmo conceito mas agora temos de utilizar o lado engastado, porque no engaste a inclinação é zero. Temos, portanto:
Passo 7
Agora vamos para a quarta integral, já considerando os valores de , e :
Essa integral se refere à linha elásticae pode ser escrita como:
Vamos aplicar o mesmo conceito mas agora temos de utilizar o lado engastado, porque no engaste a deflexão também é zero. Temos, portanto:
Logo a equação da linha elástica é igual a:
Que pode ser escrita como: