Exercícios Resolvidos de Inclinação e deslocamento por integração

Enunciado

Sabendo-se que a viga é um perfil laminado de aço e que , e , determinar a declividade em .

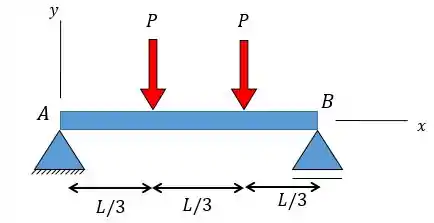
Passo 1

Essa questão é bem direta e pede para a gente achar a linha elástica. A gente só tem que achar primeiro o momento fletor antes e aplicar na equação da linha elástica:

Neste exercício é pedido apenas a equação linha estática à esquerda da força (perceba a direção de ).

A diferença aqui é que no final vamos substituir os valores para achar um resultado numérico ao invés de um resultado estilo “sopa de letrinhas”.

Passo 2

Galera, como o foco da aula é a linha elástica eu já vou colocar aqui para vocês o resultado das reações e do momento fletor:

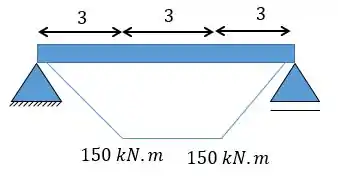
Então a equação do momento fletor pode ser dividida em três partes e será:

Para

Para

Para

Passo 3

Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:

Pessoal! Como a gente quer só a declividade em podemos pegar apenas a primeira parte:

Para

Substituindo :

Agora vamos integrar em :

Show de bola! Essa vai ser a equação da nossa angulação, mas a gente ainda precisa encontrar o valor de , vamos fazer isso utilizando a seção do meio.

Passo 4

Para a seção do meio nós vamos ter:

Para

Substituindo na equação:

Agora temos a equação da angulação para a seção do meio, e por que fizemos isso? Porque agora podemos achar o valor de , já que sabemos que a inclinação exatamente na metade é igual a zero (porque a viga é simétrica)!

Assim, vamos ter:

Passo 3

Mas a gente não quer a inclinação em ? Então vamos igualar a equação da primeira parte e da segunda parte no ponto onde elas devem ser necessariamente iguais, em !!