Determine a deflexão em da barra. Considere constante.
Passo 1
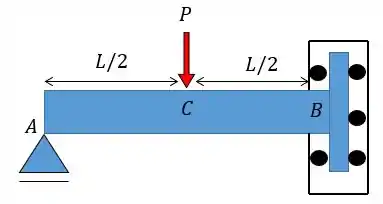
Fala, galerinha!!! Aqui o problema nos fornece uma viga apoiada num apoio de primeiro gênero na extremidade esquerda e com um apoio do tipo carrinho na extremidade direita. Devemos lembrar que esse tipo de apoio impede tanto a rotação quanto o deslocamento na horizontal porém permite o deslocamento na vertical. Então as nossas reações vão ficar assim:
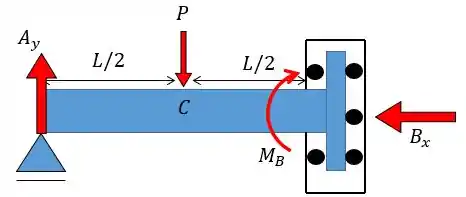
Com isso o principal é achar a função que defini o momento fletor na barra para podermos substituir na equação da linha elástica:
Passo 2
Primeiro vamos definir o sentido do eixo , essa parte é muito importante ok? Então podemos definir por exemplo da esquerda para a direita:
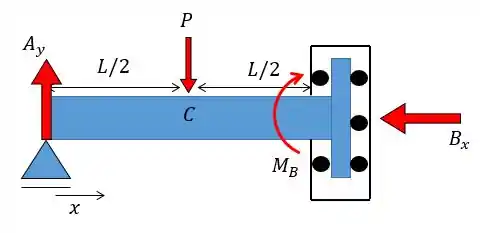
Como só existe uma força na horizonta então vamos ter que:
Logo, para as forças no eixo vertical vamos ter:
E para as momentos, aplicados em , vamos ter:
Pronto! Achamos nossas reações, agora montar o diagrama de momentos fletores ficou mais fácil:
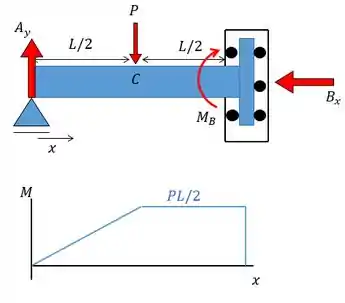
Desta forma vamos ter a função do momento fletor dada por:
Passo 3
Agora vamos partir para as integrais, lembrando que temos duas equações de momento fletor, então devemos fazer cada uma separadamente. Vamos começar com o lado esquerdo:
Substituindo
Integrando novamente:
Então para a primeira metade temos:
obs: Lembre-se que
Passo 4
Agora vamos fazer para o lado direito:
Substituindo:
Integrando novamente:
Agora também temos as duas equações do lado direito:
Falta achar só as constantes! Para isso vamos utilizar as condições de contorno.
Passo 5
A primeira condição de contorno e a mais simples de ser observada é que não há deflexão no ponto , dessa forma podemos substituir na seguinte equação:
E obter:
A segunda condição de contorno que é um pouco mais difícil de ser observada é que, o apoio do lado impede a rotação, logo podemos substituir no ponto da seguinte equação:
Substituindo:
Show de bola, mas agora acabaram as nossas condições de contorno, o que faremos?
Passo 6
No problema nós temos apenas uma barra, contínua, mas na nossa resolução nós temos o dobro de equações. Como a barra é contínua nós podemos dizer que a inclinação e deflexão do ponto será igual independetemente da equação que estamos olhando.
Dessa forma nós vamos ter que as equações das inclinações e das deflexões são iguais..
Mas é importante lembrar que isso só vale para , então vamos substituir:
Substituindo as constante que a gente já calculou:
Vamos obter:
Agora temos um sistema com duas equações e duas incógnitas, resolvendo nós vamos achar:
Passo 7
Então nossa equação da deflexão para a segunda metade é dada por:
Substituindo obtemos: