Uma viga engastada está sujeita a uma força conforme o desenho abaixo. Considerando constante encontre a equação da linha elástica. Encontre também a máxima deflexão e inclinação.
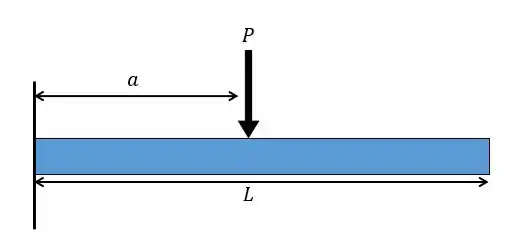
Passo 1
A gente tem que achar a linha elástica e para isso precisamos achar primeiro o momento fletor antes e aplicar na equação da linha elástica:
Lembrando que temos de utilizar as condições de contorno dadas por aquela nossa tabelinha:
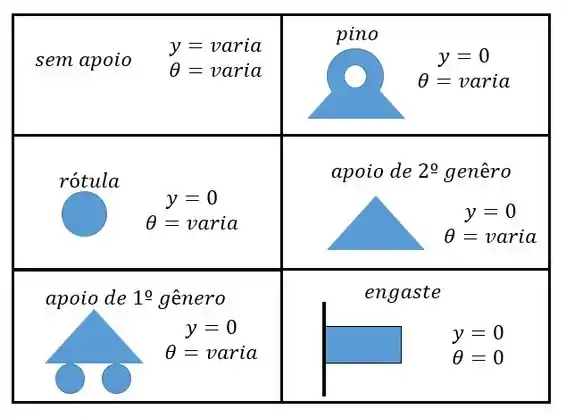
Passo 2
Para achar o momento fletor primeiro precisamos achar as forças nos apoios, para isso vamos desenhar um esquema de forças.
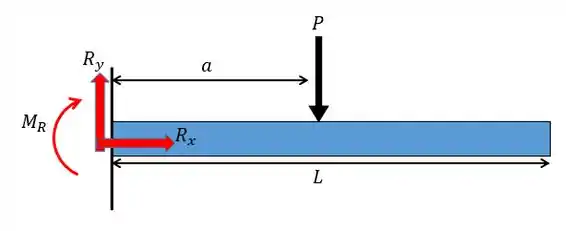
Pelas equações da estática vamos ter:
Como só existe uma força em :
Para as forças em :
Para os momentos considerando o sentido horário positivo e aplicados na extremidade engastada vamos ter:
Passo 3
Com as forças vamos poder achar o momento fletor, realizando um corte entre o engaste e a aplicação da força vamos ter:
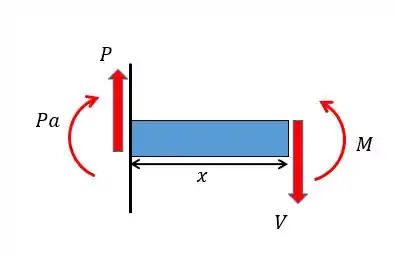
Fazendo o somatório das forças em de modo a achar a força cortante:
Agora podemos achar o momento fletor, fazendo o somatório dos momentos em torno do ponto e considerando o sentido horário positivo:
Uhulll achamos o momento!! Agora vamos achar a linha elástica!!
Passo 4
Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:
Substituindo :
Agora vamos integrar em :
Agora podemos utilizar a condição de contorno referente ao ângulo (porque ). Com isso vamos ter que a inclinação em (no ponto de engaste) é nula. Se quiser volta lá na tabelinha pra conferir =D
Substituindo os valores vamos ter:
Logo,
Nossa equação fica da forma:
Com isso já da para achar a maior inclinação. Podemos perceber que essa função é estritamente crescente, sendo assim o maior valor da inclinação ocorrerá no maior ponto de ou seja :
Passo 5
Agora vamos derivar a equação novamente para achar a linha elástica:
Como no engaste () não temos deflexão vamos ter:
Sendo assim
E a equação da linha elástica é dada por:
Passo 6
Da mesma forma que a inclinação, a linha elástica vai ser estritamente crescente. Sendo assim, vamos ter o maior valor em obtendo: