Determine o conjunto solução da seguinte inequação:
Passo 1
A primeira coisa que vamos fazer, é colocar esses caras na mesma base.
Daí vamos escrever:
Passo 2
Como a nossa base é maior do que 1, podemos escrever:
Daí, teremos:
Temos aí um quociente entre uma equação do 2º grau e uma do 1º grau
Passo 3
As raízes de serão . E essa função é crescente.
A raiz de será igual a 0.Essa função do primeiro grau também será crescente.
Agora, vamos construir a nossa tabelinha
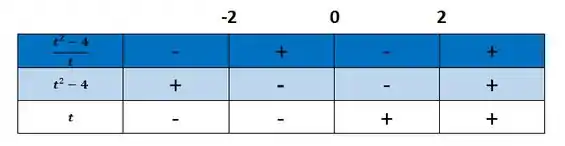
Vale observar que não podemos colocar o , pois isso geraria uma divisão por zero, uma indeterminação matemática.
Sendo assim, nosso conjunto solução será:
Resposta
Exercícios de Livros Relacionados
Demonstrar:Se a = 0 e b = 0 , então a^2 = b^2 se e somente se a = b .